Adam: A Method for Stochastic Optimization

October 27, 2025 | 330 words | 2min read

Paper Title: Adam: A Method for Stochastic Optimization

Link to Paper: https://arxiv.org/abs/1412.6980

Date: 22. Dec. 2014

Paper Type: Optimizer, Learning Techniques, Deep Learning

Short Abstract: In this paper, the famous Adam optimizer is introduced: a first-order, gradient-based optimization method that uses adaptive estimates of momentum. It generalizes well across different architectures and tasks and outperforms many optimizers that came before it.

1. Introduction

Many problems in the fields of science and engineering can be formulated as the optimization of some scalar objective function requiring maximization or minimization.

If this objective function is differentiable, then gradient descent can be used, which is relatively efficient since it only requires first-order derivatives.

Many of these functions can also be stochastic — for example, they might be defined on subsets (mini-batches) of data. In such cases, stochastic gradient descent (SGD) can be used for improved efficiency. The objective function can also be noisy, such as when using techniques like dropout.

This paper focuses on high-dimensional, stochastic, differentiable objective functions, where higher-order optimization methods perform poorly due to the curse of dimensionality.

In light of this, the paper proposes Adam, a first-order optimization method that requires little memory. This method computes individual learning rates for every parameter, based on estimates of the first and second moments of the gradient. As such, it combines the advantages of three methods:

• RMSprop: learning individual learning rates for each parameter
• Adagrad: using past gradients to adapt the learning rate
• Momentum: accelerating convergence by smoothing gradients

2. Method

The algorithm updates exponential moving averages ( m_t ) of the gradient and the squared gradient ( v_t ), where hyperparameters control the exponential decay rates of these moving averages.

3. Experiments

To empirically evaluate their optimizer, the authors tested it on different architectures — e.g., logistic regression and neural networks — and on different datasets such as MNIST and IMDB movie classification.

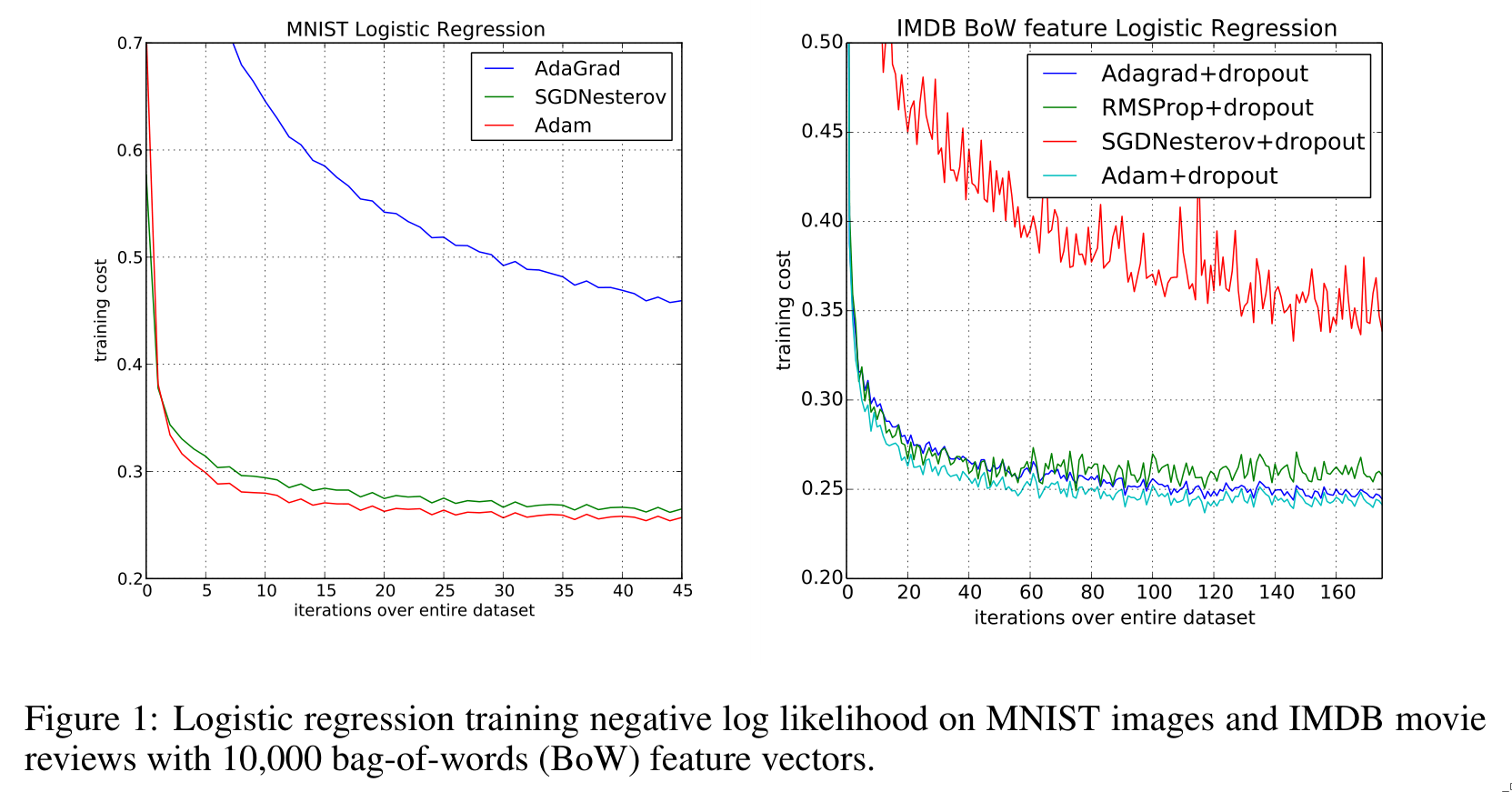
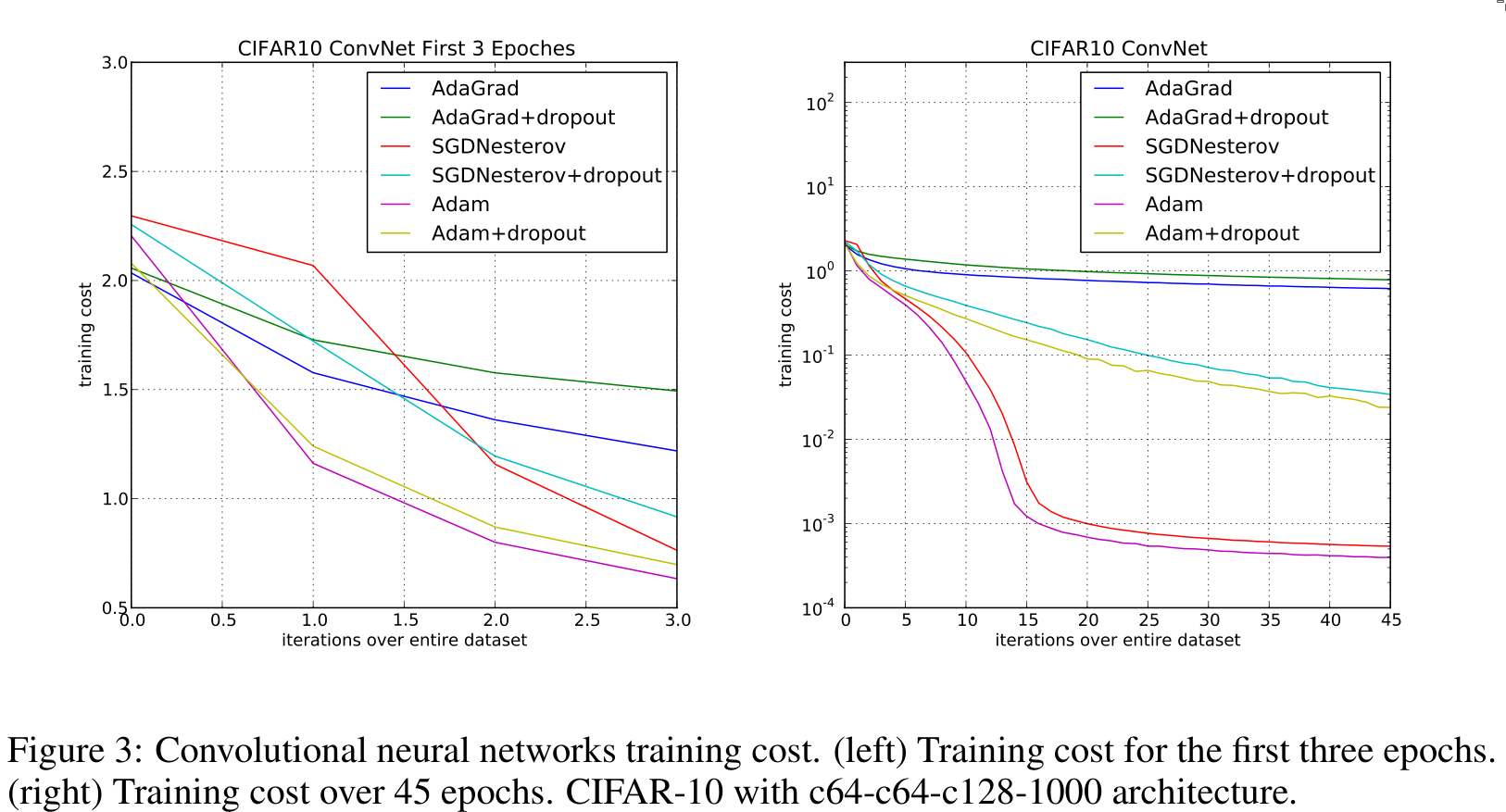
4. Conclusion

The introduced Adam optimizer is efficient and performs well, not only proven theoretically but also demonstrated empirically.

reply via email