AdamW: Decoupled Weight Decay Regularization

October 27, 2025 | 436 words | 3min read

Paper Title: AdamW: Decoupled Weight Decay Regularization

Link to Paper: https://arxiv.org/abs/1711.05101

Date: 14. Nov. 2017

Paper Type: Optimizer, Learning Techniques, Deep Learning

Short Abstract: This paper introduces the AdamW optimizer, an improvement on the Adam optimizer that additionally incorporates weight decay.

1. Introduction

Adaptive, gradient-based optimizers such as AdaGrad, RMSprop, and Adam have become the default choice for training feed-forward neural networks. Still, state-of-the-art performance on many image datasets, such as CIFAR-10 and CIFAR-100, is often achieved using SGD.

Why is that?

The authors of this paper suggest that one reason lies in the way L₂ regularization and weight decay are used in conjunction with optimizers. They show that a major reason SGD outperforms Adam is that L₂ regularization, which is commonly applied to both methods, works much better with SGD. Instead, they argue, Adam should use weight decay.

They arrive at the following observations:

• L₂ regularization and weight decay are not identical. This belief spread because under certain parameter choices, the two are equivalent for SGD, but this is definitely not true for adaptive optimizers like Adam.
• L₂ regularization is not effective in Adam. Adam performs worse than SGD when L₂ regularization is used. Instead, weight decay should be used with Adam.
• Weight decay is equally effective in both SGD and Adam.
• Adam benefits substantially from a learning rate scheduler. The common belief that Adam does not need a global learning rate schedule (because it adapts per-parameter rates) is false, using a global scheduler, such as cosine annealing, improves Adam’s performance.

2. Weight Decay and Decoupled Weight Decay

Weight decay works as follows:

$$ \theta_{t+1} = (1 - \lambda)\theta_t + \alpha \Delta f_t(\theta_t) $$

where \( \lambda \) defines the rate of weight decay per step.

For SGD, this is equivalent to L₂ regularization, but only if the regularization term is set to \( \lambda / \alpha \).

The authors propose using decoupled weight decay, where weights are updated separately from the gradient update. This decouples \( \lambda \) (weight decay) and \( \alpha \) (learning rate).

What is the intuitive difference between weight decay and L₂ regularization?

• Both mechanisms push weights closer to zero at a similar rate.
• In L₂ regularization, we use the sum of the gradients of the loss function and the regularizer.
  • This causes weights associated with large gradients to be regularized by a smaller relative amount than others.
• In decoupled weight decay, only the gradient of the loss function is used.
  • All weights are regularized at the same rate.

3. Experiments

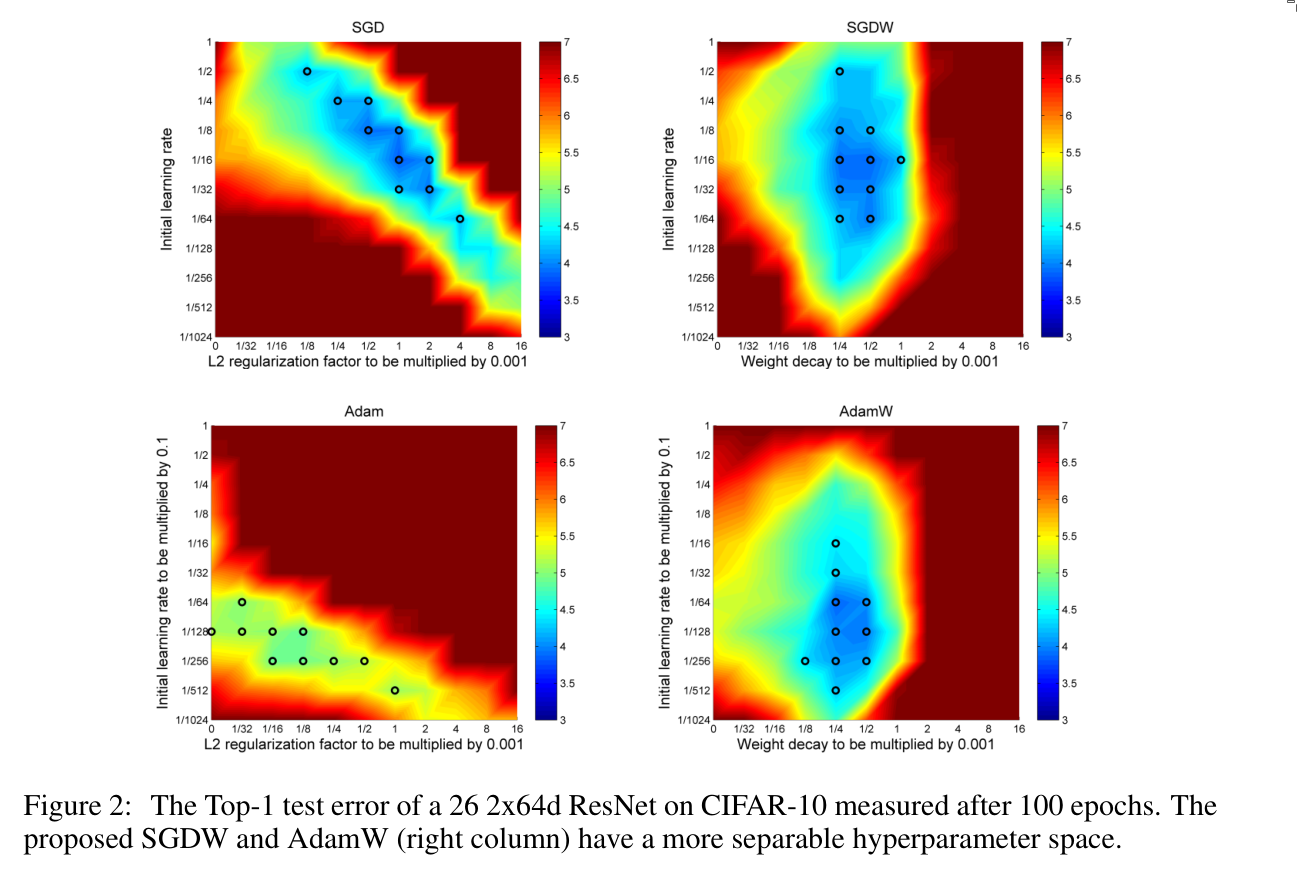
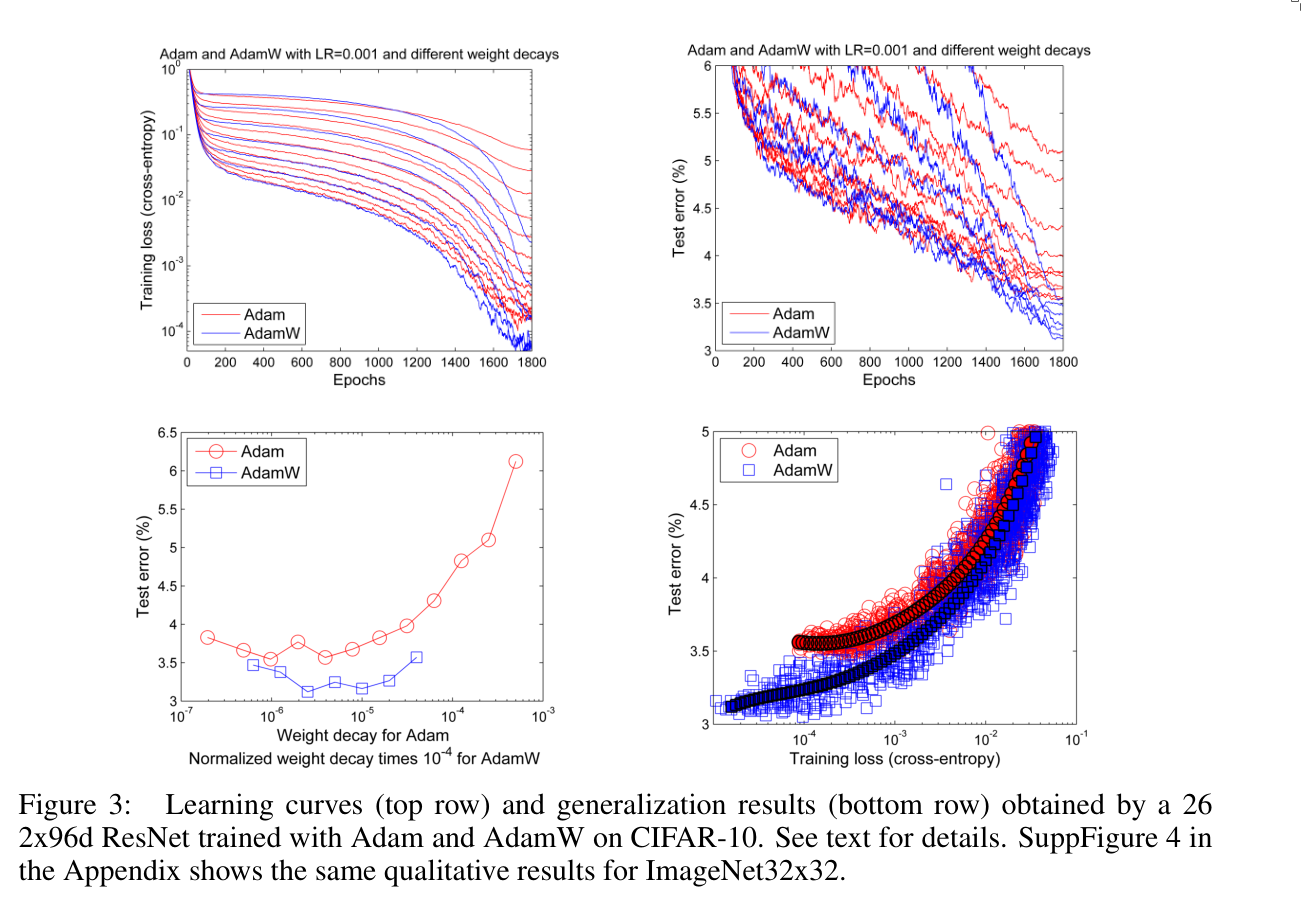
4. Conclusion

AdamW was shown to perform better, both theoretically and empirically, than Adam, demonstrating improved generalization and optimization efficiency.