ADAPT-pNC: Mitigating Device Variability and Sensor Noise in Printed Neuromorphic Circuits with SO Adaptive Learnable Filters

September 30, 2025 | 433 words | 3min read

Paper Title: ADAPT-pNC: Mitigating Device Variability and Sensor Noise in Printed Neuromorphic Circuits with SO Adaptive Learnable Filters

Link to Paper: https://ieeexplore.ieee.org/document/10992786

Date: 21 May. 2025

Paper Type: Training, Neuromorphics, Noise, Internet-of-Things, Data-Augmentation

Short Abstract: In this paper, the authors expand their previously introduced printed temporal processing neuromorphic circuits (pTPNCs) with device-variation–aware training.

1. Introduction

See the previous paper introduction for a general motivation.

Another problem in printed electronics is that the manufacturing process is not as accurate as lithography. As such, printed devices can often vary significantly from one to another. In addition, analog signals are very noise-susceptible, especially time sequences, leading to errors in the input data that, if not taken into account, can propagate to the output.

Until now, there has not been a serious effort to include both input-data variation and device variability in printed analog neuromorphic circuits (pNCs).

In this work, the authors introduce a variation-aware printed temporal processing block (pTPB) to address these issues. In addition, they use data-augmentation techniques to mitigate noisy inputs.

2. Background

See the previous paper.

3. Robust-Aware Adaptive Temporal Processing Block

In wearable devices, such as those for stress detection, absolute values of sensory data are not as important as the temporal changes.

In previous approaches, static first-order low-pass filters (LPFs) in pNCs were used to filter out high-frequency noise, but they are often insufficient. Thus, the authors instead utilize a learnable second-order filter (SO-LF) within pNCs.

This can be achieved by using two learnable resistors and capacitors connected back-to-back.

The values of the resistors in the crossbar, which act as both weights and biases, can be learned using their variation-aware learning scheme.

3.1 Modeling of the Second-Order Filter

For the exact mathematical model—i.e., the relationship between the resistors and crossbar values—see the paper.

3.2 Variation-Aware Training of the Proposed Second-Order Filter

The resistor (R) and capacitor (C) are trainable and subject to variation in the manufacturing process. Thus, they are modeled using random variables during training:

with a distribution representing the variation in the manufacturing process.

The training objective is then to minimize the expected loss.

3.3 Variation in Input Sensor

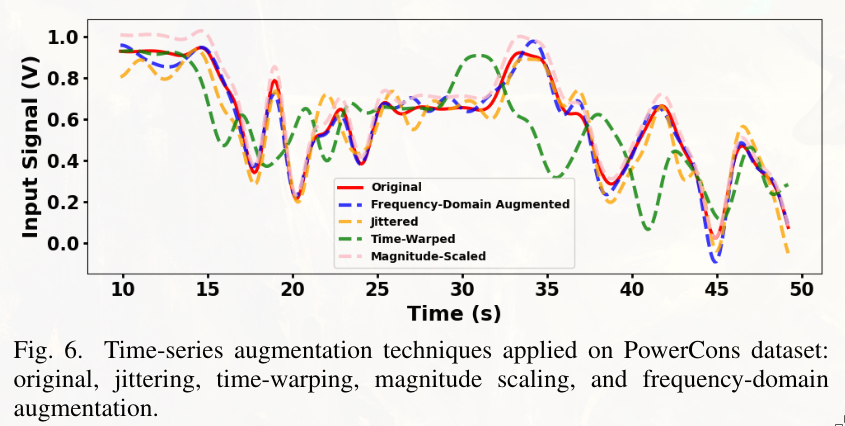
To improve robustness, data augmentation on the input data is used. For time-frequency datasets, they employ signal distortion, random cropping to mimic data availability, jittering, and magnitude scaling.

4. Evaluations

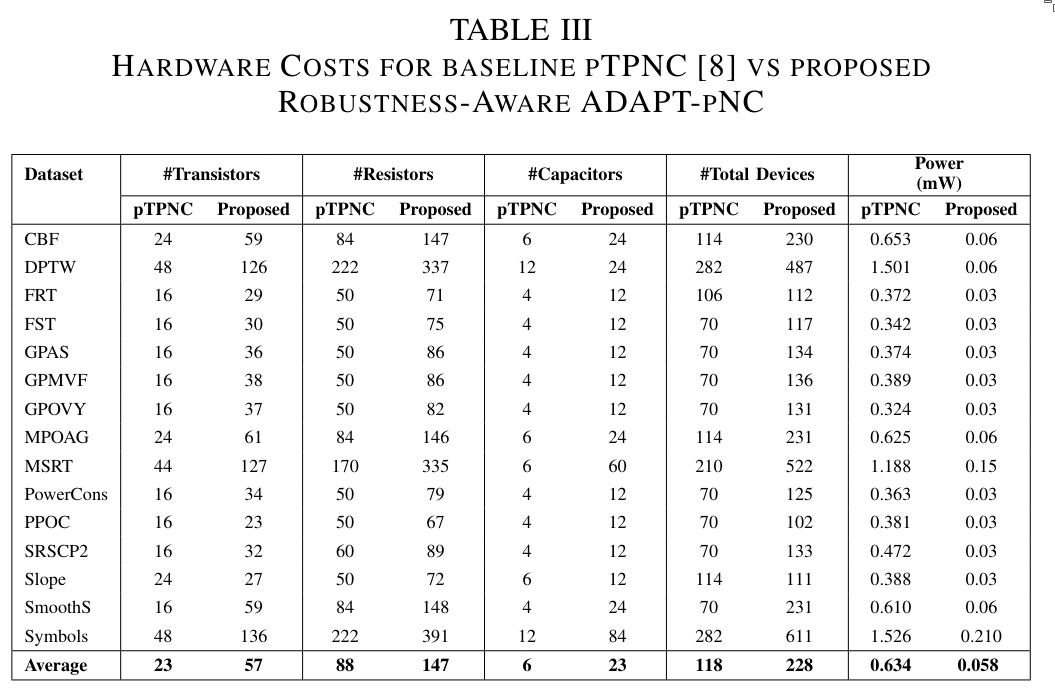
5. Conclusion

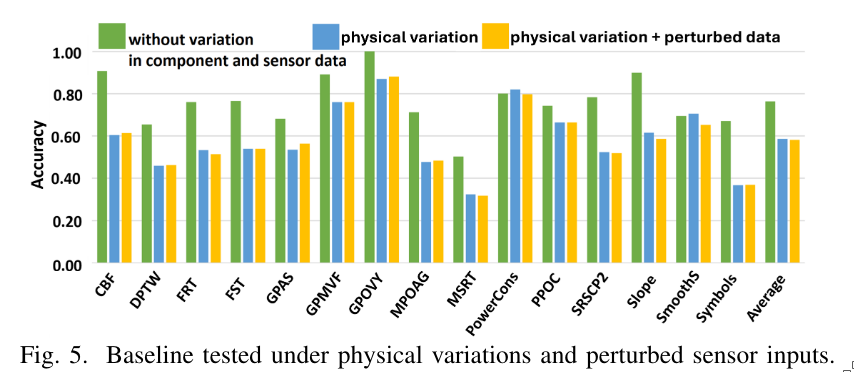
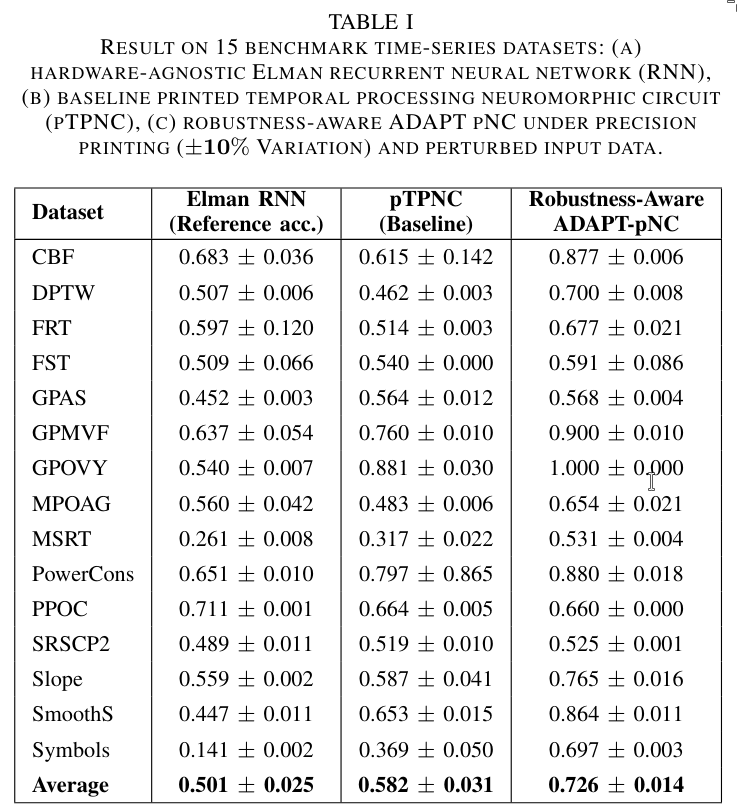
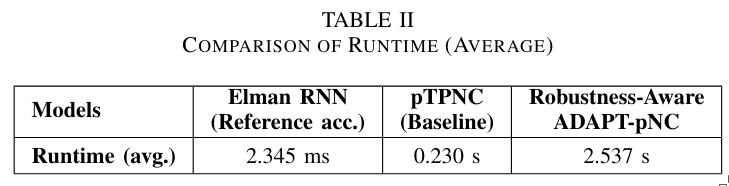
Their experiments show that the accuracy improvement from the Elman RNN to the pTPNC (baseline) is approximately 15%. For the robustness-aware ADAPT-pNC, this improvement increases to approximately 45%. Additionally, ADAPT-pNC requires approximately 1.9× more devices compared to the pTPNC (baseline).

reply via email