Attention is All You Need

December 1, 2023 | 1,124 words | 6min read

Paper Title: Attention is All You Need
Link to Paper: https://arxiv.org/abs/1706.03762
Date: 12. Jun2 2017
Paper Type: LLM, Architetcure, Attention
Short Abstract:
“Attention is All You Need” is a landmark paper that helped usher in the modern era of AI. It proposes the Transformer architecture, which relies on attention mechanisms to weight all the tokens in a sequence based on the current token.

1. Introduction

Recurrent Neural Networks (RNNs) and later models like LSTMs have long dominated the domain of sequence modeling, such as language modeling and machine translation.

However, these models rely on a hidden state that the next time step depends on. This inherently sequential nature prevents significant speedups through parallelization.

In this work, the authors propose the Transformer architecture—a model without recurrence that relies entirely on global attention. This design enables significant parallelization and achieves state-of-the-art results in machine translation.

2. Model Architecture

Most sequence-to-sequence models follow an encoder-decoder structure. The encoder maps an input sequence \(x\) to a sequence of continuous representations \(z\). For example, it converts a sentence (a sequence of words) into a sequence of token vectors that the model can process.

Given the tokens \(z\), the decoder then generates an output sequence \(y\). The Transformer also follows this architecture, with the encoder shown on the left side of the figure and the decoder on the right.

2.1 Encoder and Decoder Stacks

Encoder

• Stack of \(N = 6\) layers
• Each layer consists of:
  • Multi-head self-attention mechanism
  • Position-wise fully connected feed-forward network
• Residual connections around each sub-layer
• Layer normalization applied after each sub-layer
• All layers use a fixed dimensionality \(d = 512\)

Decoder

• Also a stack of \(N = 6\) layers
• In addition to the sub-layers in the encoder, each decoder layer includes:
  • Multi-head attention over the encoder’s output
• Residual connections and layer normalization as in the encoder
• Masking is applied to prevent the decoder from attending to subsequent positions
  • This ensures that the token at position \(i\) can only depend on known outputs up to position \(i - 1\)

2.2 Attention

The attention mechanism takes as input a query, key, and value. When applied across all tokens, these become matrices, each with dimension \(d_k\).

To compute attention, we take the dot product of the query and key, scale it by \(\sqrt{d_k}\), and apply the softmax function. The result is a weight matrix that we use to weight the values:

$$ \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V $$

The matrices \(Q\), \(K\), and \(V\) in the first attention layer are computed as:

$$ Q = W_Q X \quad K = W_K X \quad V = W_V X $$

The interpretation of the attention mechanism is as follows: The query matrix can be understood as the model asking, for each input token (e.g., a word), “What should I pay attention to?” The key matrix provides the potential answers to that question. The dot product between the queries and keys measures the similarity between them—i.e., how relevant each key is to a given query.

In essence, each query specifies what it wants to attend to, the keys represent all available options, and the dot product tells us which keys (tokens) are most relevant. The resulting weights are then applied to the value matrix, which contains the actual content the model processes.

2.3 Multi-Head Attention

Instead of performing a single attention function, it is practically useful to perform it multiple times in parallel. This is similar to how convolutional neural networks use multiple filters to detect different features. In the same way, using multiple attention heads allows the model to focus on different aspects of the input.

For example, one attention head might focus on punctuation (e.g., commas and periods) to help understand syntax, while another might focus on named entities like people or places.

Multi-head attention works as follows:

As shown, we perform attention multiple times—each producing an output called a head. These heads are then concatenated and passed through a final linear layer. Together, this forms one multi-head attention layer, whose output can then be used as input for further layers.

In this paper, the authors use \(h = 8\) parallel attention heads.

2.4 Applications of Attention in Our Model

Attention is used in three different ways:

• Encoder-Decoder Attention: In these layers, the queries come from the previous decoder layer, while the keys and values come from the encoder’s output. This allows every position in the decoder to attend to all positions in the input sequence. (In the diagram, this is the multi-head attention block receiving input from the left half—i.e., the encoder.)
• Self-Attention in the Encoder: Each position in the encoder can attend to all positions in the previous layer of the encoder.
• Self-Attention in the Decoder: Similarly, self-attention layers in the decoder allow each position to attend to all previous positions—including itself. To prevent the decoder from attending to future tokens (which have not yet been generated), masking is applied in the scaled dot-product attention, setting attention weights to \(-\infty\) where needed.

2.5 Position-wise Feed-Forward Networks

In addition to the attention mechanism, each layer in the Transformer architecture includes a fully connected feed-forward network, which is applied separately to each position. This is computed as:

$$ \text{FFN}(x) = \max(0, xW_1 + b_1)W_2 + b_2 $$

2.6 Embeddings and Softmax

To convert sequences of input tokens into model-dimensional vectors, an embedding layer is used. At the output stage, the softmax function is applied to the decoder’s output to generate a probability distribution, which is then used to predict the next token in the sequence during generation.

2.7 Positional Encoding

Since the Transformer architecture does not rely on recurrence, it lacks built-in information about the order of tokens. To address this, the authors add positional encodings to the input embeddings at the bottom of both the encoder and decoder stacks.

These encodings are defined as:

$$ PE_{\text{pos}, 2i} = \sin\left(\frac{\text{pos}}{10000^{2i/d_{\text{model}}}}\right) \\ PE_{\text{pos}, 2i+1} = \cos\left(\frac{\text{pos}}{10000^{2i/d_{\text{model}}}}\right) $$

Where pos is the position in the sequence, and i is the dimension index.

3. Why Self-Attention?

There are three main advantages to using self-attention:

• Total complexity per layer: Compared to other architectures like RNNs or CNNs, the Transformer has higher per-layer complexity. However, it performs much better during training due to its parallelism.
• Parallelization: The Transformer architecture allows for significantly more parallel computation compared to recurrent models, making it much faster to train.
• Long-range dependencies: Transformers are particularly effective at capturing long-range dependencies in sequences, which RNNs often struggle with.

4. Experiments

4.1 Training and Inference

Training Details

• Dataset: WMT 2014 (English-German)
• Hardware: 8 NVIDIA P100 GPUs
• Training duration: 4 days
• Optimizer: Adam
• Learning rate schedule: Warmup steps
• Regularization: Residual Dropout, Label Smoothing

Inference

• Tasks: English-to-German Machine Translation, evaluated also on Penn Treebank
• Decoding: Beam search with beam size = 21

4.2 Results

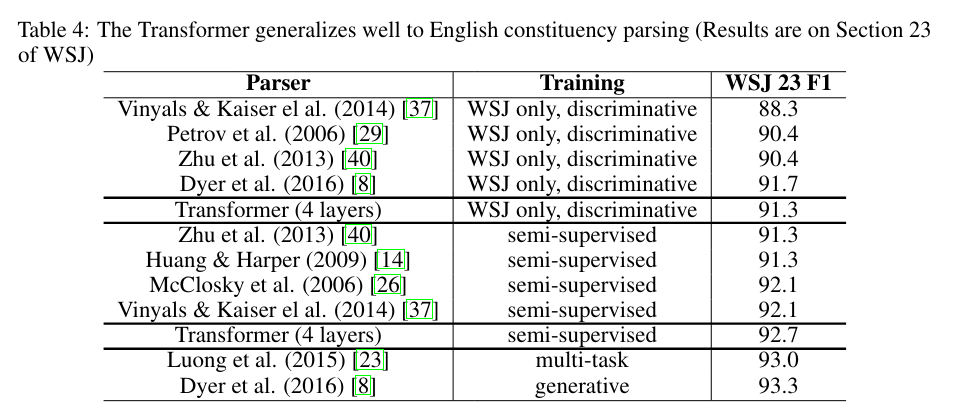
5. Conclusion

Transformers are great!