Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

November 4, 2025 | 576 words | 3min read

Paper Title: Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

Link to Paper: https://arxiv.org/abs/1502.03167 1;129B

Date: 11. Feb 2015

Paper Type: Architecture, Learning Techniques, Deep Learnin

Short Abstract: This paper introduces the famous BatchNorm technique, which helps reduce internal covariate shift and thus leads to faster convergence during training and more stable gradients.

1. Introduction

Popular optimization algorithms in deep learning such as Stochastic Gradient Descent (SGD) or Adam have been proven to be very effective in training deep networks.

These optimizers, instead of iterating over the entire training set before performing an update step, use mini-batches. These mini-batches are used to approximate the gradient of the loss function over the full training set.

Using mini-batches has the advantage, compared to using a single example, that parallelism can be exploited and the resulting gradients are more stable. It also has an advantage over using the entire training set as one batch, since such large batch sizes are often not feasible due to memory limitations.

One problem in deep learning is that the input of each layer affects the preceding layers. Because of that, a small change in the last layer can lead to large changes in the earliest layers.

Another problem is covariate shift. Covariate shift occurs when the input distribution of a system changes to a new distribution.

This notion of covariate shift can be extended to parts of a network. Consider the following network:

$$ l = F_2(F_1(u, \theta_1), \theta_2) $$

where \(F_1\) and \(F_2\) are arbitrary transformations (e.g., layers in a neural network) and \(\theta_1, \theta_2\) are learnable parameters to minimize the loss function \(l\).

Learning \(\theta_2\) can be viewed as if the input \(x = F_1(u, \theta_1)\) is fed into this subnetwork.

Therefore, the properties of the input distribution that make efficient training possible—such as having the same distribution between training steps—should also apply to the sub-networks. In other words, it is advantageous if we maintain the same distribution throughout the entire neural network, because then \(\theta_2\) does not have to compensate for changes introduced by the first layer.

Fixed distributions have another advantage when using sigmoid functions: when using sigmoid or similar activation functions, very little is learned at the extremes. This can easily happen if the distributions throughout the layers are not consistent, as it can lead to unequal magnitudes of activation changes across layers.

2. Method

Internal covariate shift is the change in the distribution of network activations due to updates of the network parameters during training.

Resolving this issue by stabilizing the distribution can drastically speed up training, particularly for very deep networks.

To address this issue, the authors introduce Batch Normalization (BatchNorm). In BatchNorm, the current batch is used to calculate an approximation of the mean and standard deviation of the training set, which are then used in each layer to normalize and rescale the data. Through this, every layer maintains a more stable and fixed distribution.

To ensure this normalization does not artificially limit the network, two scaling parameters are introduced—one for the mean and one for the standard deviation—which the network can learn during training.

3. Experiment

Experiments were conducted on the MNIST dataset using both feedforward and convolutional neural networks.

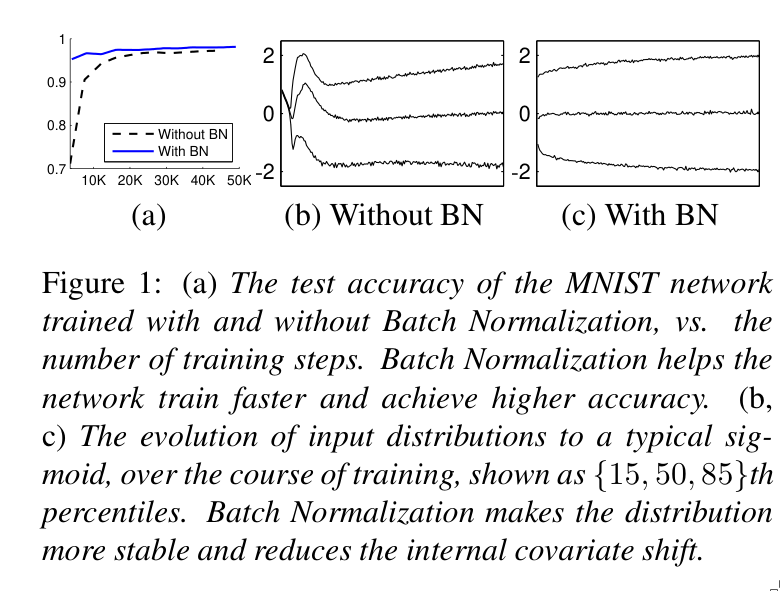
Experiments have shown that when BatchNorm is used, dropout can be drastically reduced or even omitted entirely. In addition, higher initial learning rates and stronger decay can be used effectively.

4. Conclusion

BatchNorm works well in practice and significantly reduces training time.