Dropout: A Simple Way to Prevent Neural Networks from Overfitting

October 31, 2025 | 488 words | 3min read

Paper Title: Dropout: A Simple Way to Prevent Neural Networks from Overfitting

Link to Paper: https://dl.acm.org/doi/10.5555/2627435.2670313

Date: 01. Jan. 2014

Paper Type: Deep-Learning, Machine Learning

Short Abstract: Dropout is a regularization technique used to address overfitting in large networks. The key idea is to randomly drop units along with their connections from the network during training.

1. Introduction

Deep neural networks consist of many layers and neurons. When insufficient data is available, they are prone to overfitting.

Many techniques have been developed to help mitigate this issue, such as L1 and L2 regularization and soft weight sharing.

If unlimited computational resources were available, the best way to regularize a network would be to train multiple models with all possible hyperparameter configurations and then average their outputs. In small networks, this can be approximated, but for large networks, it is infeasible.

This infeasibility arises because training multiple large networks is prohibitively expensive. Moreover, combining models is only useful if they are sufficiently different—either in architecture or in training data. The former is difficult, as each architecture requires its own hyperparameter tuning, and the latter is often impossible due to limited data availability. Even if it were possible, inference time would become extremely high.

Dropout addresses both of these issues: it helps prevent overfitting and approximates the combination of many different neural network architectures.

Dropout works by randomly removing units (and their connections) from the network during training. Whether a unit is kept or dropped is decided independently for each unit based on a fixed probability.

The idea of dropout is not limited to feedforward neural networks—it can also be applied more generally to graphical models such as Boltzmann machines.

2. Motivation

A closely related, but slightly different motivation for dropout comes from thinking about successful conspiracies. Ten conspiracies each involving five people is probably a better way to create havoc than one big conspiracy that requires fifty people to all play their parts correctly. If conditions do not change and there is plenty of time for rehearsal, a big conspiracy can work well, but with non-stationary conditions, the smaller the conspiracy the greater its chance of still working. Complex co-adaptations can be trained to work well on a training set, but on novel test data they are far more likely to fail than multiple simpler co-adaptations that achieve the same thing.

3. Model Description

A feedforward neural network can be described as:

$$ z = Wy + b $$

$$ y = f(z) $$

With dropout, the operation becomes:

$$ r \sim \text{Bernoulli}(p) $$

$$ y = r * y $$

$$ z = Wy + b $$

$$ y = f(z) $$

During testing, the weights are scaled by ( p ). The resulting neural network is then used without dropout.

4. Experiments

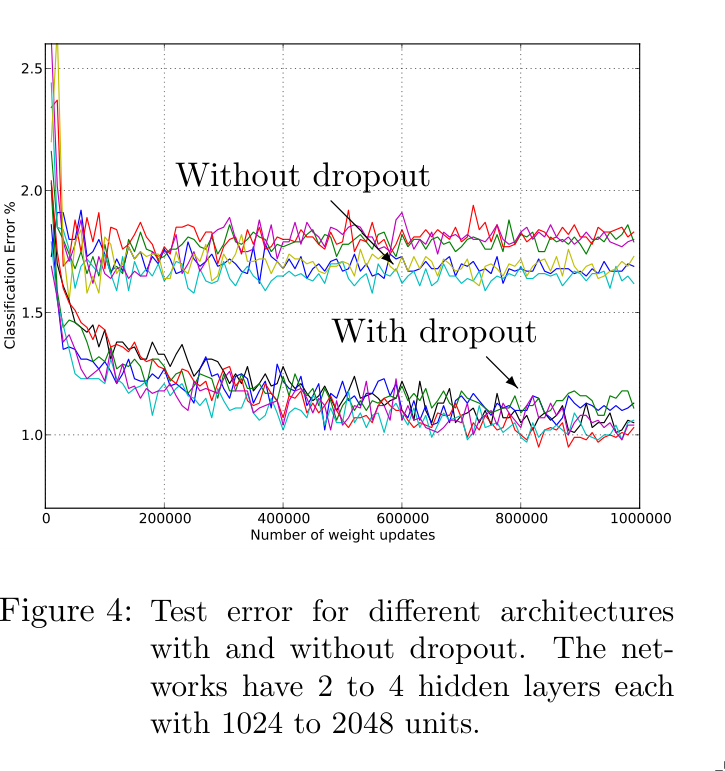
5. Conclusion

Dropout helps reduce overfitting. When using dropout, the learning rate should typically be 10–100 times higher than normal, and higher momentum values should be used.