Notes from the Wired

Communication-Efficient Learning of Deep Networks from Decentralized Data

Published: November 10, 2024

Paper Title: Communication-Efficient Learning of Deep Networks from Decentralized Data
Link to Paper: https://arxiv.org/pdf/1602.05629
Date: January 26, 2023
Paper Type: Deep Learning, Training Methods, Decentralized Training
Short Abstract:
Almost everyone nowadays possesses mobile devices that produce a wealth of data, which could be used to train models, such as for predicting the next word typed on a keyboard. However, privacy concerns make conventional training approaches unfeasible. The authors introduce Federated Learning, a decentralized approach where data never leaves the device.

1. Introduction

Mobile devices have various sensors, such as cameras, microphones, and GPS, and are often used, resulting in large amounts of available data. However, the sensitive nature of this data makes storing it centrally a considerable risk (even anonymizing the data doesn’t offer much protection).

In the Federated Learning technique, data is not stored centrally; instead, it stays on the devices. Their architecture uses a central server that coordinates participating clients. The clients use their local data to update the model on their devices, and only the update is uploaded to the central server.

This approach allows training on sensitive data without risking exposure. It also reduces the attack surface to only the client side.

Federated Learning - For a problem to benefit from federated learning, it should have two properties: (1) training on real-world data provides an advantage over training on proxy data, and (2) the data is privacy-sensitive. For supervised tasks, labels can be inferred from user interaction.

Two examples are image classification (e.g., identifying photos that may be viewed again) and language models for touchscreen keyboards. In both cases, potential data sources, such as user photos and keyboard inputs, are privacy-sensitive. Proxy data may not perform well; for example, Wikipedia images differ too much from local images.

Privacy - Centralizing even anonymized data can still expose users to risks. In federated learning, only updates need to be transmitted to the server, which contain less information than the raw data.

Federated Optimization vs. Distributed Optimization - There are several key differences in federated optimization:

For this paper, the authors assume a synchronous update schedule consisting of communication rounds. They have \(K\) clients.

The general overview of the algorithm is as follows:

  1. At the beginning of each round, a random fraction \(C\) of clients is selected. The server sends the current model parameters to these clients because adding more clients yields diminishing returns.
  2. After receiving the model parameters, each client computes updates using their data and sends the update to the server.
  3. The server applies these updates, and the process repeats.

In distributed learning (e.g., in data centers), communication costs are minor. In federated learning, communication costs dominate all other costs. Some communication challenges include:

There are two ways to decrease communication costs: (1) increase parallelism (i.e., use more clients per round), and (2) increase computation on the device (i.e., each device performs multiple computations instead of one). Parallelism helps only up to a certain point.

2. The \(\text{FederatedAveraging}\) Algorithm

The authors build on stochastic gradient descent (SGD). This can be done naively by calculating a single batch per device per round, but it requires many steps to converge.

In this approach, they select a fraction of the clients \(C\) each round and compute the gradient of the loss over all data these devices hold. The higher \(C\), the larger the global batch count, so \(C=1\) represents full-batch gradient descent (not stochastic anymore).

The central server aggregates the gradients \(g_k\) and applies them to the model parameters \(w_{t+1} := w_{t} - \alpha \sum \frac{n_k}{n} g_k\), where \(n\) is the total global batch size, and \(n_k\) is the size of each participating client.

An equivalent update is \( w_{t+1} := w_t - \alpha \sum \frac{n_k}{n} w^k_{t+1}\), meaning each client takes a local step using its data, and the server averages the resulting models. With this setup, computation can be increased by performing more local steps before uploading the model, a method called FederatedAveraging.

This algorithm is controlled by these parameters:

If you choose \(B = \infty\), \(E = 1\), you have federated SGD.

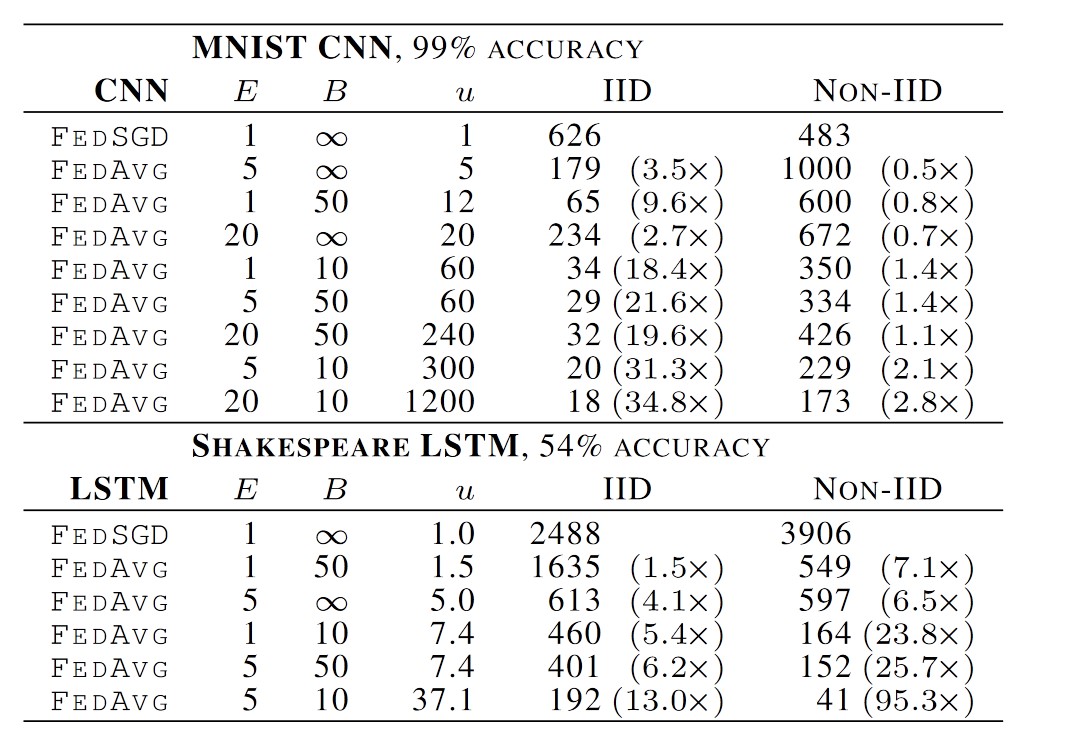
If models on different clients are initialized with different seeds, the algorithm won’t work. They need to be initialized with the same seed.

3. Experimental Results

The algorithm was applied to the CIFAR-10 and MNIST image classification datasets and an LSTM for word prediction based on The Complete Works of William Shakespeare.

For MNIST, they tested two data distributions: IID (shuffled data) and Non-IID (data sorted by digit label and divided into shards assigned to clients).

They determined the optimal learning rate for SGD through grid search.

Parallelism - The higher \(C\) (number of clients per round), the better the computational efficiency but the worse the convergence rate, so they chose \(C=0.1\) for further testing.

Increasing computation per client - Provided \(B\) is large enough to fully utilize client hardware, lowering it further offers no benefit.

They also tested the algorithm on CIFAR-10, achieving an 85% accuracy after 2000 communication rounds (with the state-of-the-art being 96%).

For the MNIST dataset, entries show the number of communication rounds necessary to reach an accuracy of 97%.
Entries indicate the number of communication rounds required to achieve a target accuracy.

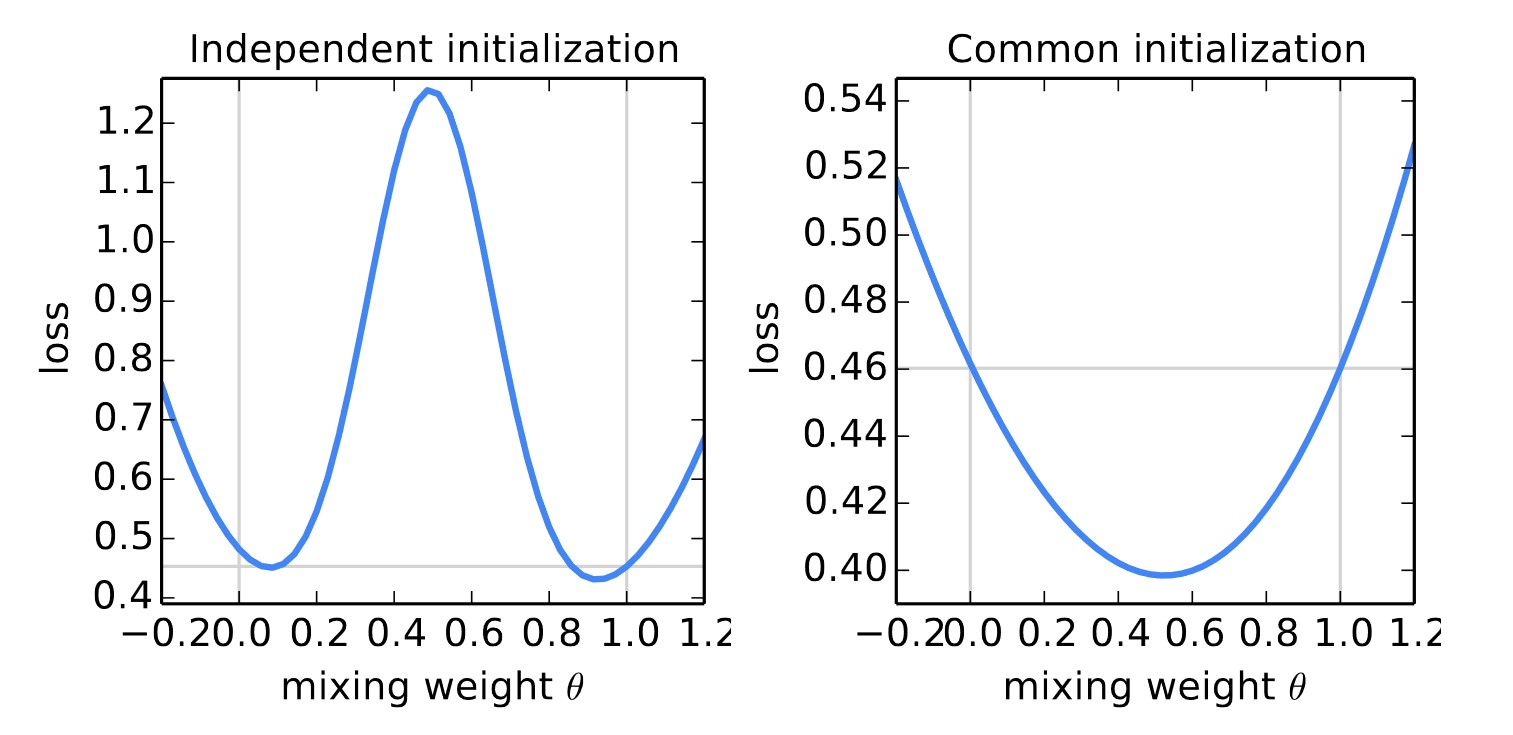
These results indicate that averaging multiple client model parameters leads to convergence after multiple rounds, proving the technique’s effectiveness.

4. Conclusion

Through these experiments, the authors demonstrate that their algorithm can train a model while keeping privacy-sensitive data secure.

▲
Made with Hugo, website licensed under CC BY-NC-SA 4.0.