Generative Adversarial Imitation Learning

March 26, 2025 | 628 words | 3min read

Paper Title: Generative Adversarial Imitation Learning
Link to Paper: https://arxiv.org/abs/1606.03476
Date: 10. June 2016
Paper Type: RL, Imitation Learning
Short Abstract:
In standard reinforcement learning, we have a reward function that we can use to train our model. But what if we don’t have one? Two approaches to address this are behavior cloning and inverse reinforcement learning, each with distinct advantages. This paper proposes a new framework for directly extracting policy from data.

1. Introduction

Imitation learning is the problem where we want an agent to learn a given task using expert data, without requesting additional data from the expert during training.

There are two common approaches to imitation learning. The first is behavior cloning, where the agent learns the task in a supervised manner by imitating expert trajectories. The second is inverse reinforcement learning (IRL), where the algorithm seeks a cost function under which the expert trajectories are optimal.

Behavior cloning, while simple, has the disadvantage of requiring a large amount of data and is susceptible to covariate shift, a phenomenon where model performance degrades when encountering states outside the training distribution.

On the other hand, inverse reinforcement learning (IRL) suffers from the issue of prioritizing certain trajectories from the training data more than others, leading to compounding errors. Additionally, it requires reinforcement learning at every step, making it computationally expensive.

An algorithm that could learn directly from data without first training a reward model—and with lower computational cost—would be beneficial. In this paper, the authors introduce Generative Adversarial Imitation Learning (GAIL), a framework that learns policies directly from data using Generative Adversarial Networks (GANs).

2. Abridged Theory

2.1 Background

Inverse Reinforcement Learning (IRL) - Given an expert policy \( \pi_E \), we aim to find the reward/cost function \( c \) under which it is optimal:

$$ \max_c \left( \min_{\pi \in \Pi} - H(\pi) + \mathbb{E}_{\pi}(c(s, a)) \right) - \mathbb{E}_{\pi_E}(c(s, a)) $$

where \( H(\pi) = \mathbb{E}_{\pi}(-\log(\pi(a | s))) \) is the discounted causal entropy. This equation assigns a low cost to the expert policy and a high cost to other policies.

2.2 Theorem

IRL is the dual of an occupancy measure matching problem—in other words, traditional IRL is equivalent to finding a policy that matches the expert trajectories. Adding a constant regularization term to this equation results in apprenticeship learning. By using a more generalized regularization term, we obtain an equation that can be trained using the GAIL algorithm.

2.3 Algorithm

We have a generative model \( G \) and a discriminator model \( D \). The job of \( D \) is to distinguish between data generated by \( G \) and expert trajectories. The job of \( G \), on the other hand, is to generate data that fools the discriminator into believing it came from an expert trajectory.

The goal of the algorithm is to find a saddle point for the following expression:

$$ \mathbb{E}_{\pi}(\log(D(s,a))) + \mathbb{E}_{\pi_E}(\log(1 - D(s,a))) - \lambda H(\pi) $$

After initializing \( D \) and \( G \), the algorithm alternates between:

1. An Adam gradient step to increase the equation with respect to \( D \).
2. A TRPO step to decrease the equation with respect to \( \pi \).

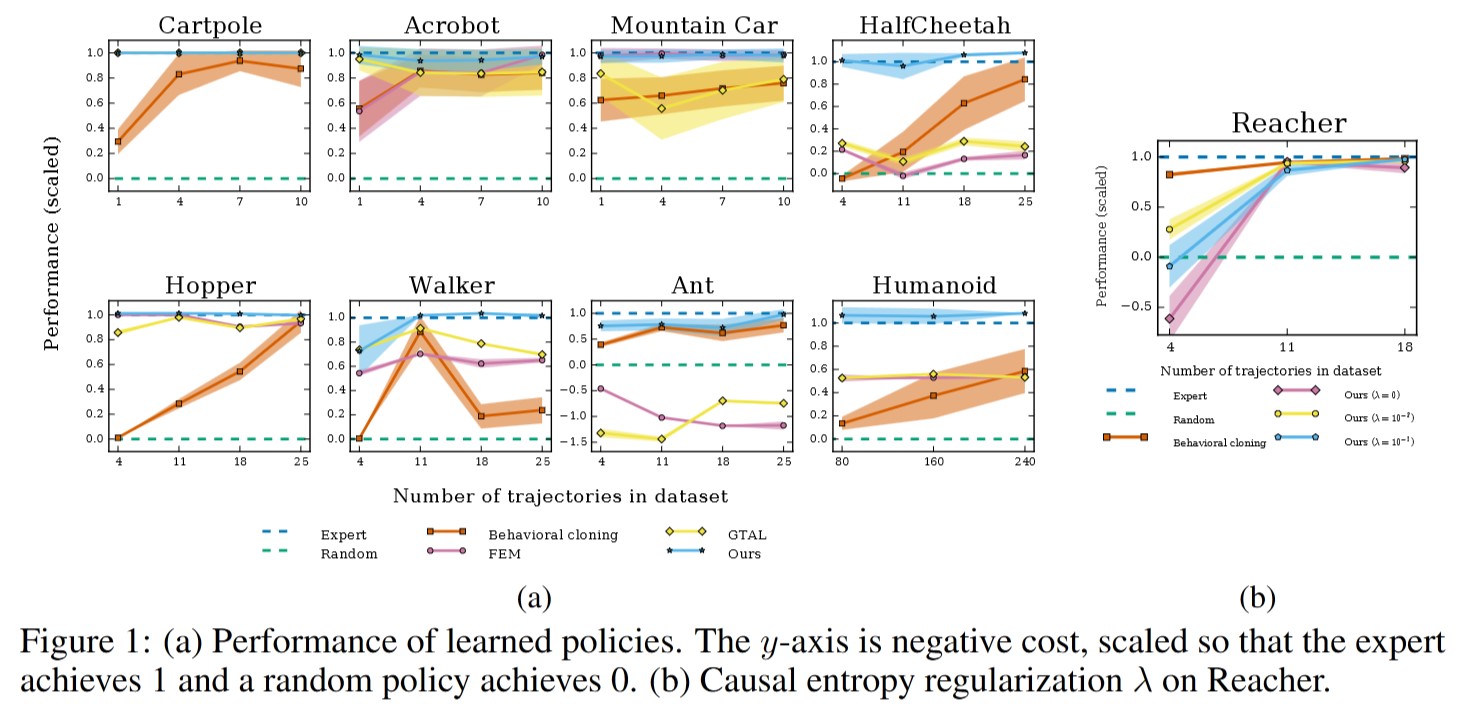
3. Experiments and Results

The algorithm was evaluated on physics-based control tasks simulated in the MuJoCo environment, with the true cost function defined by OpenAI Gym. For each task, the algorithm was tested against three baselines:

• Behavior Cloning (BC)
• Feature Expectation Matching (FEM)
• Game-Theoretic Apprenticeship Learning (GTAL)

For all tasks, the same neural network (NN) architecture was used: a two-hidden-layer network with 100 neurons per layer and Tanh activation functions. The networks were initialized randomly.

4. Conclusion

GAIL outperforms most other available methods and requires less expert data. However, it heavily relies on a large number of environment interactions during training.