Hardware Efficient Weight-Binarized Spiking Neural Networks

June 27, 2025 | 1,329 words | 7min read

Paper Title: Hardware Efficient Weight-Binarized Spiking Neural Networks
Link to Paper: https://ieeexplore.ieee.org/document/10136955
Date: 17. April 2023
Paper Type: SNN, Architetcurre, Hardware, FPGA
Short Abstract:
The author introduces a weight-binarized spiking neural network (WB-SNN), in which both the weights and spikes are represented using only binary values (0 or 1). This architecture is implemented on an FPGA, demonstrating significant memory savings.

1. Introduction

Spiking Neural Networks (SNNs) are often preferred over traditional Artificial Neural Networks (ANNs), both for efficiency reasons and for their greater biological plausibility.

SNNs typically use one of two schemes to encode information:

• Firing rate encoding, where a neuron fires if enough spikes accumulate within a certain time frame.
• Latency encoding, where neurons that fire earlier are given preference.

Both of these encoding schemes enable event-driven computation, meaning neurons are only updated when a spike occurs. This leads to reduced power consumption. Additionally, SNNs can decompose complex operations into simpler, more efficient ones. For example, a weighted sum can be represented as a series of additions over time. This property is especially useful when deploying SNNs on neuromorphic hardware such as FPGAs or chips like IBM’s TrueNorth.

However, as SNNs scale up, they require more parameters and, consequently, more memory. This presents a challenge for neuromorphic systems, which typically distribute memory across different physical locations. Efficiently accessing this distributed memory is difficult and demands careful hardware design. The more parameters an SNN has, the more this becomes a bottleneck.

This memory problem is often more severe in SNNs than in ANNs due to several factors:

• SNNs process information over time using spikes (binary events), requiring the state of each neuron to be tracked across multiple time steps — leading to increased memory usage.
• SNNs exhibit sparse activity, resulting in irregular memory access patterns that are harder to optimize.
• Neuromorphic hardware uses distributed memory structures to mimic the architecture of the brain, making memory access even more complex.

To address these issues, Binarized Neural Networks (BNNs) were introduced. BNNs represent both weights and activations using binary values (“+1” and “−1”), which reduces memory usage. Additionally, this allows multiplications like \(w \cdot x\) to be replaced with simple XNOR operations, which are far more hardware-efficient.

The author proposes an extension of this idea called the Weight-Binarized Spiking Neural Network (WB-SNN). In WB-SNNs, weights remain binarized as “+1” and “−1”, but spikes are simplified to binary values: “1” for a spike and “0” for no spike (instead of using “−1”). This means that only two values are needed in total: “+1” is represented as 1, and “−1” as 0—making the system fully binary.

In this design, the XNOR operation used in BNNs is replaced by a priority encoder (PE), which is shared among all neurons in a layer. This further improves hardware efficiency.

2. Background

2.1 Spiking Neural Networks (SNNs)

SNNs imitate biological neurons. Just like biological neurons, a neuron in an SNN receives spikes from other neurons, which are added to its internal membrane potential. When this membrane potential exceeds a certain threshold, the neuron fires.

There are different neuron models that can be used. One commonly used model is the perfect integrate-and-fire (PIF) model:

$$ v_i = \int \sum_f W_{i,f} S_j(t) \, dt $$

where \(v_i\) is the internal membrane potential of neuron \(i, W_{i,j}\) is the weight connecting neuron \(j\) to neuron \(i\) in the current layer, and \(S_j(t)\) is the spike input from neuron \(j\), which is binary (either 0 or 1).

Because of the event-driven nature of SNNs and the binary nature of \(S_j\), we can replace the multiplication by an integral and thus by a sum. This means costly hardware multiplications can be avoided.

2.2 Binarized Neural Networks (BNNs)

The idea of BNNs stems from the desire to replace arithmetic operations with bit-wise operations for efficiency. This is possible if the weights are binary as well.

In BNNs, weights and activations are either -1 or +1, which are represented by 1 and 0 respectively in hardware. This allows multiplication to be replaced by a simple XNOR operation.

If we want to convert a traditional ANN into a BNN, this can be done either by using the sign function or through stochastic optimization, where weights are mapped to -1 or +1 according to the following probability distribution:

$$ \sigma(x) = \min\left(1, \max\left(0, \frac{x + 1}{2}\right)\right) $$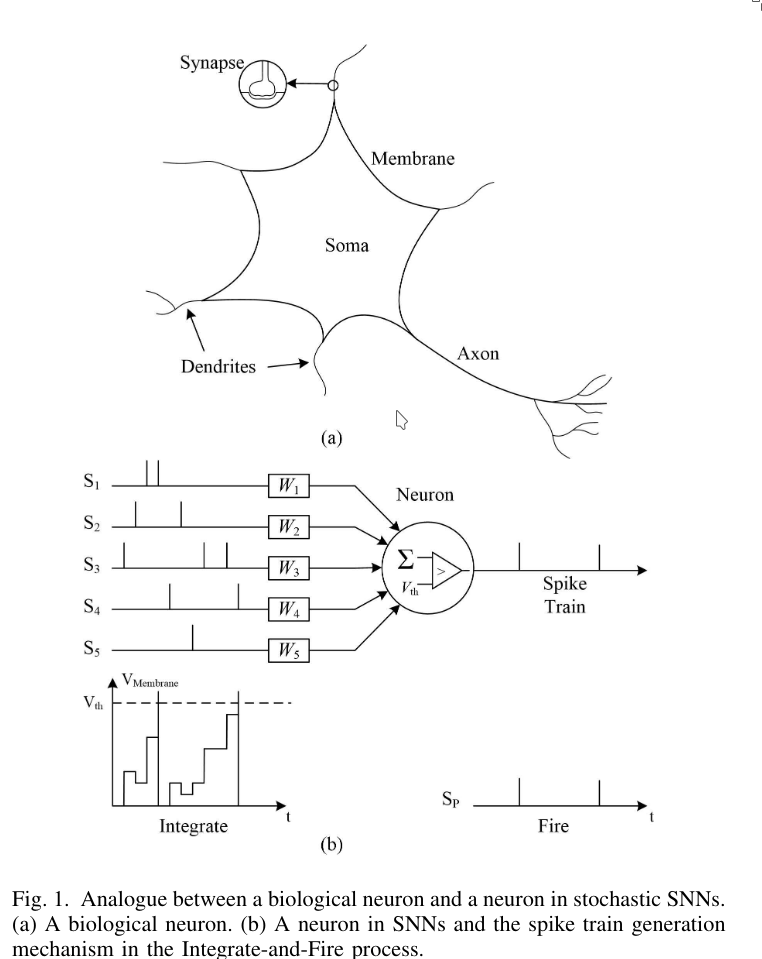

3. WB-SNNs

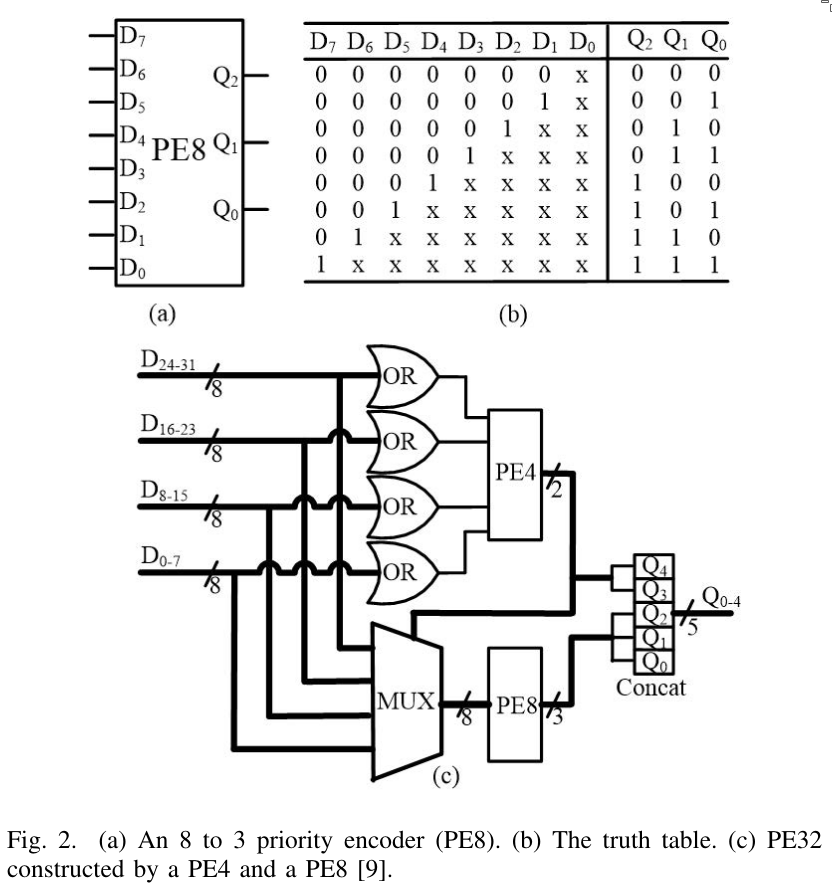
3.1 A Priority Encoder (PE)

A priority encoder is a component that takes multiple input lines and outputs the binary number corresponding to the input line that first had a spike. If multiple spikes occur simultaneously, the last input line has the highest priority.

The priority encoder is used to identify the index of an active neuron. The least significant input line $D_0$ has no impact on the output and is used to indicate when there is no input spike.

In addition to the PE, the system uses a priority reset (PRI) circuit, which prevents repeated encoding of the same bit. After the PE encodes the bit with the highest priority, the PRI clears that bit.

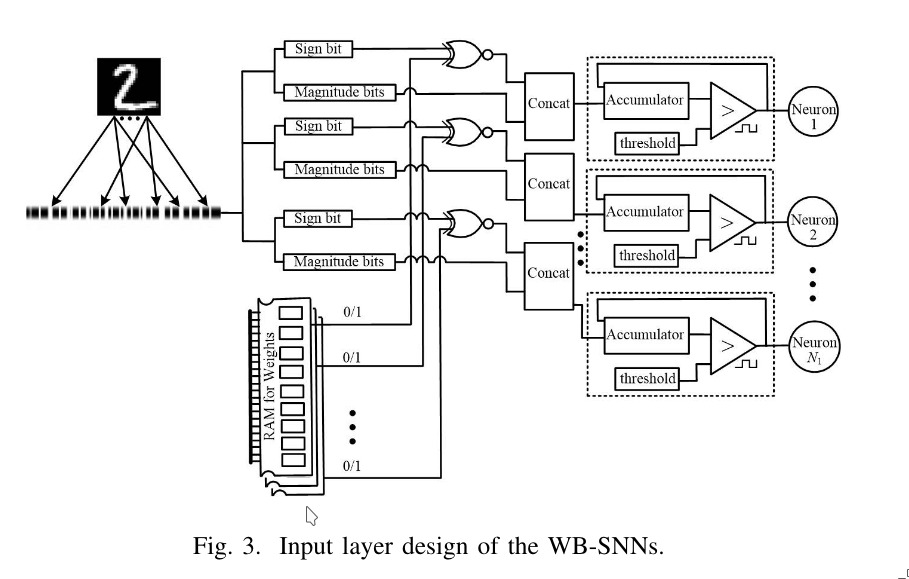
3.2 The Input Layer

The WB-SNN takes images as input, which are not originally in spike format. Therefore, the input layer transforms the images into spike format.

If the input image contains many zero pixel values, the PE & PRI blocks are used to select only the non-zero pixels, skipping accumulation of zeros. If most of the pixels are non-zero, the PE & PRI blocks can be removed and all values are used as input.

These two scenarios help reduce inference latency while saving hardware resources.

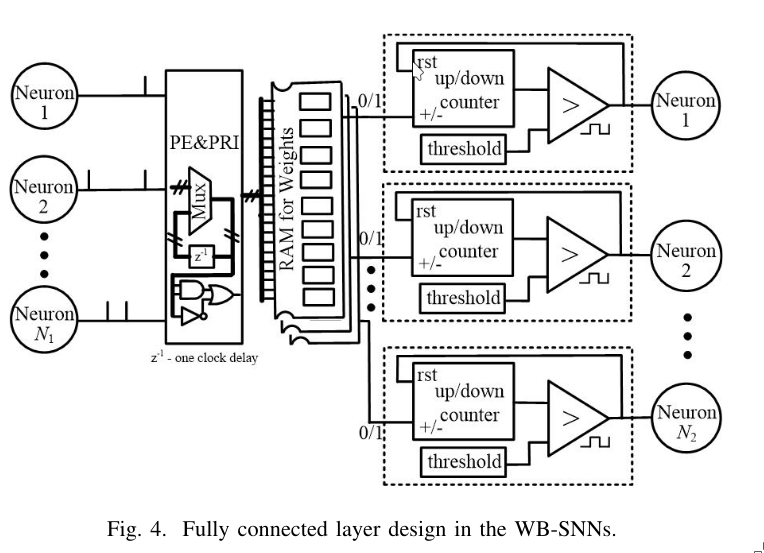
3.3 Design of the Fully Connected Layer

In a fully connected (FC) layer, all neurons from the previous layer are connected to the PE & PRI block, which transfers the active status of each input neuron to random access memory (RAM), where the weights are stored.

An up/down counter is used to track the internal membrane potential. If it receives a 1, it counts up; if it receives a 0, it counts down. When the membrane potential crosses a threshold, the neuron fires.

For each active input, the index is used to read the corresponding weight \(w\) from RAM. If the weight is:

• +1 → the up/down counter increments (i.e., \(+1 \times 1 = +1\))
• −1 → the counter decrements (i.e., \(-1 \times 1 = -1\))

Compared to conventional FC layers, only neurons with active outputs are selected and processed because of the PE & PRI blocks. This reduces energy consumption and inference latency.

4. Experiments

4.1 Preliminary

• The WB-SNN was implemented on an FPGA.
• It was trained and tested on the MNIST dataset.
• A classic MLP feed-forward architecture was used.
• Performance was compared to traditional MLP models trained on GPUs.
• \(L_2\) norm regularization was applied for better accuracy.
• Multiple models were trained with dense layers of 63, 127, 255, 511, and 1023 nodes.

4.2 Results

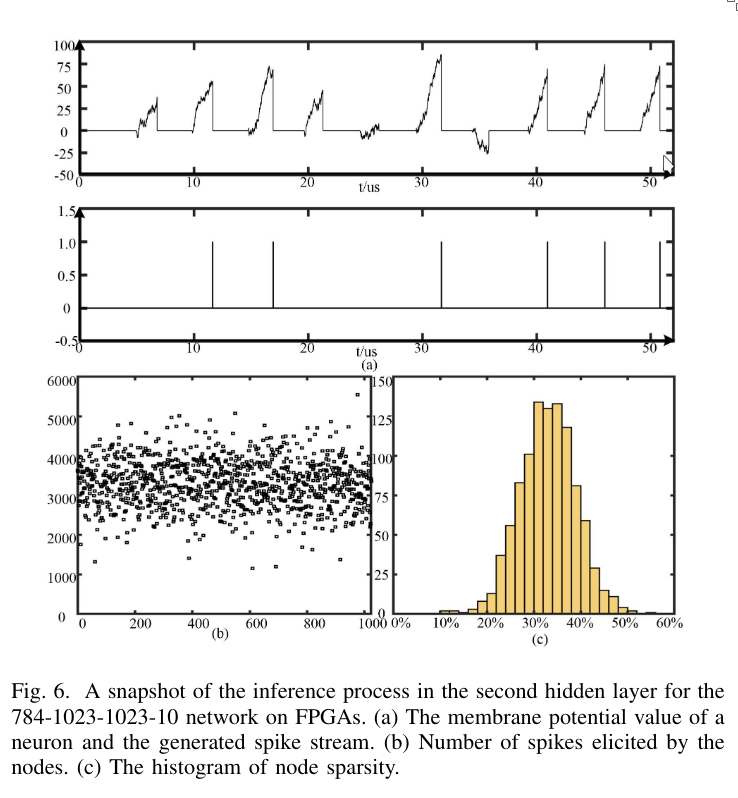
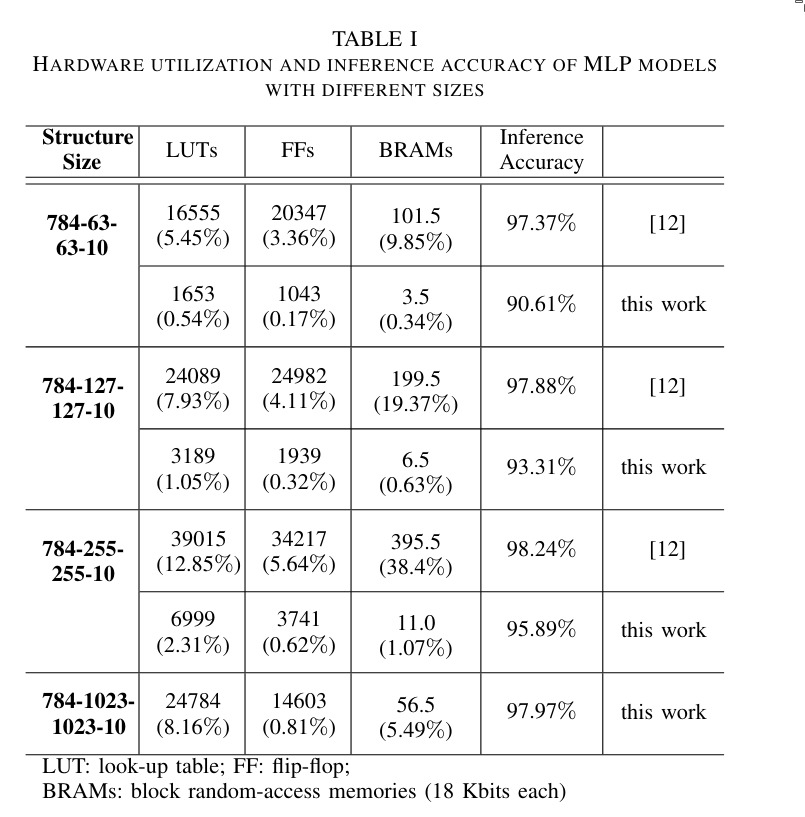
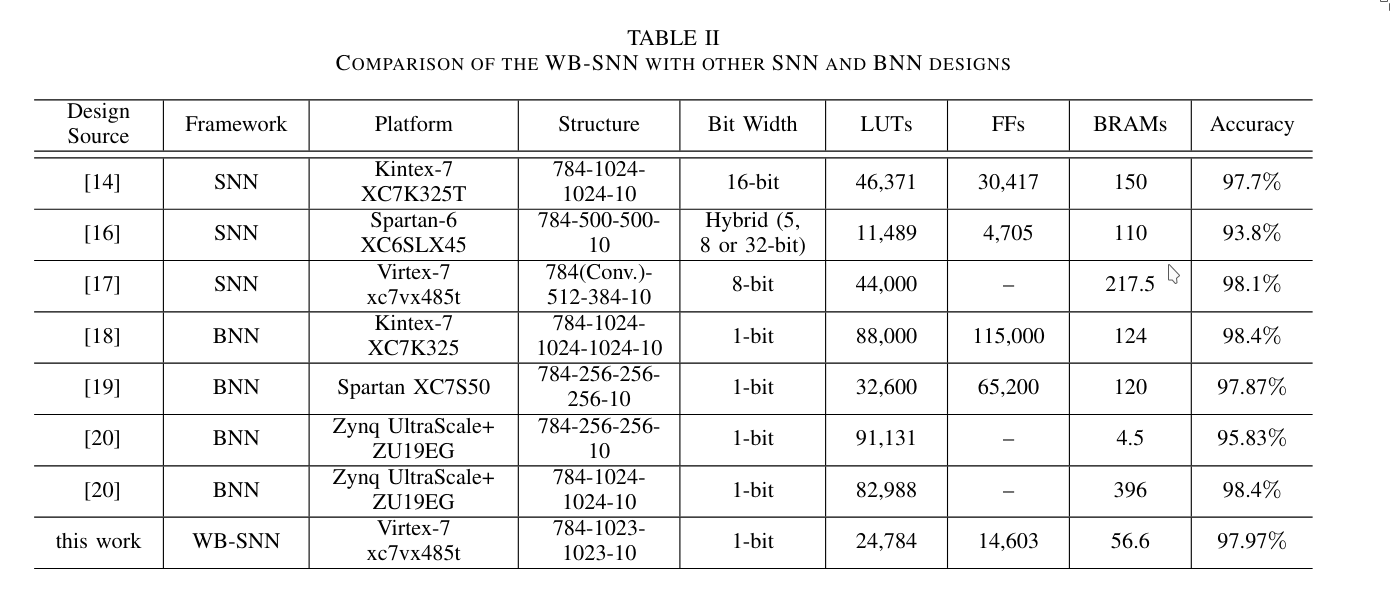
5. Conclusion

WB-SNN is a hardware-efficient SNN architecture that uses binarization to reduce memory consumption. It employs a priority encoder as the basis for its layers. The model was evaluated on the MNIST dataset and implemented on an FPGA. It achieves state-of-the-art performance while requiring significantly fewer resources.

---

My Thoughts

What I felt was missing is a comparison of how much more efficient this architecture is compared to traditional ANNs, conventional SNNs, and BNNs. A chart showing power consumption and accuracy across these different models would be very informative, especially to evaluate both inference and training efficiency.

This paper mainly shows that the WB-SNN needs less memory, which is interesting, but power efficiency would be an even more compelling metric.

Another point concerns the fully connected layer design. Because the priority encoder (PE) selects spikes sequentially by priority, if multiple spikes arrive simultaneously, the PE encodes the most significant data lane first, then the next, and so forth. This introduces a sequential processing bottleneck. Seems a bit weird; I’ve read that this operation is very fast (only 1 clock cycle) and thus not a big deal, but I’m not sure.