Kademlia: A Peer-to-peer Information System Based on the XOR Metric

July 2, 2025 | 1,239 words | 6min read

Paper Title: Kademlia: A Peer-to-peer Information System Based on the XOR Metric Link to Paper: https://dl.acm.org/doi/10.5555/646334.687801 Date: 07. March 2002 Paper Type: Network, Peer-to-Peer, Architectures, Decentralized Systems, File sharing Short Abstract: The authors propose Kademlia, a peer-to-peer architecture that can be used for file sharing. It employs a distributed hash table with the XOR metric.

1. Introduction

Kademlia is a peer-to-peer Distributed Hash Table (DHT) with a number of advantageous characteristics:

• It minimizes the number of configuration messages sent for nodes to learn about each other.
• Configuration information spreads automatically.
• It is parallel and asynchronous, thus avoiding timeout delays.
• The algorithm is secure against some DDoS attacks.
• These properties can be formally proven.

Like other DHTs, Kademlia uses 160-bit keys, typically generated by a hash function such as SHA-1. Each node participating in the Kademlia system has a unique 160-bit node ID. Nodes store <key, value> pairs, where the key typically maps to the ID of nodes that are “close” in the network.

To determine closeness, Kademlia uses the XOR metric on the node IDs. To find other nodes, Kademlia uses a single, consistent routing algorithm.

2. System Description

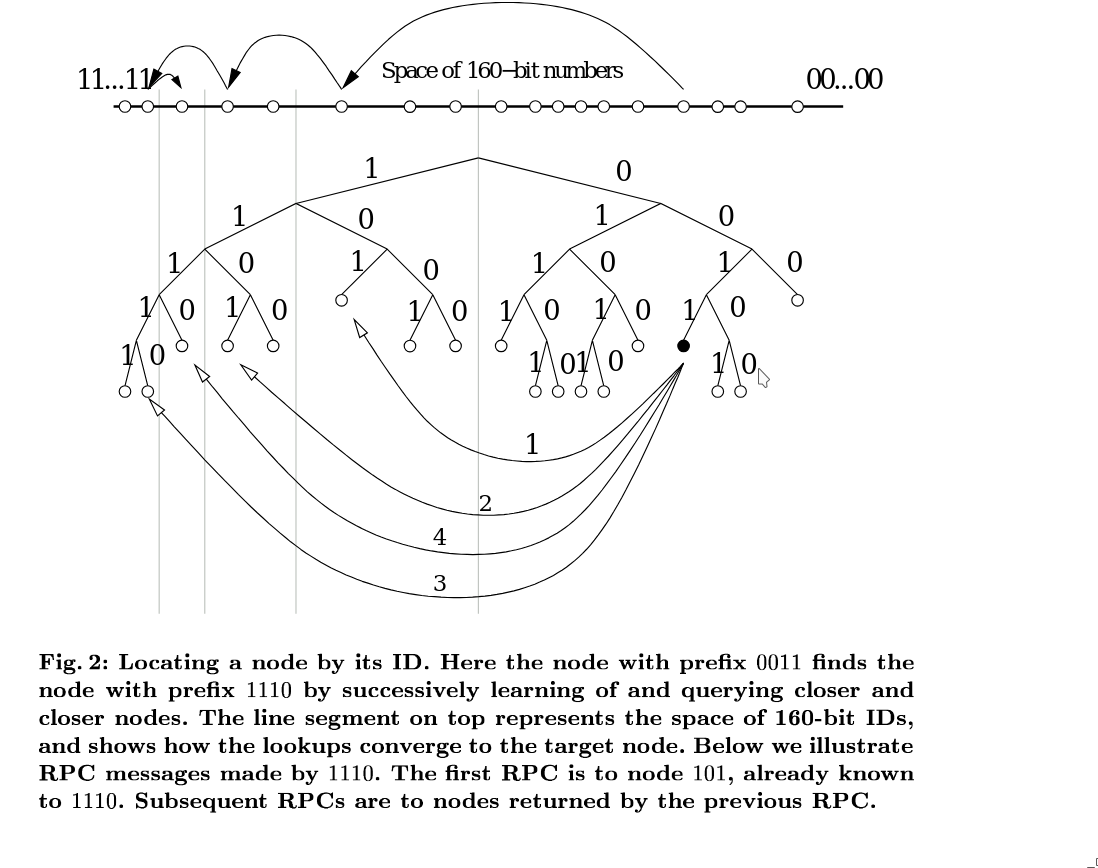
As in other decentralized systems, Kademlia consists of multiple nodes, each with a unique ID. These IDs are used in a lookup algorithm to find successively closer nodes to a desired target node.

One can imagine how a Kademlia node sees the network as a binary tree, with the leaves representing other nodes, and the path to each leaf consisting of its binary ID.

For any given node, the tree is conceptually divided into subtrees that do not contain the node itself. The process begins with the highest-level subtree, which includes half of the entire binary space that does not contain the current node. The next subtree consists of half of the remaining binary space that still excludes the current node, and so on.

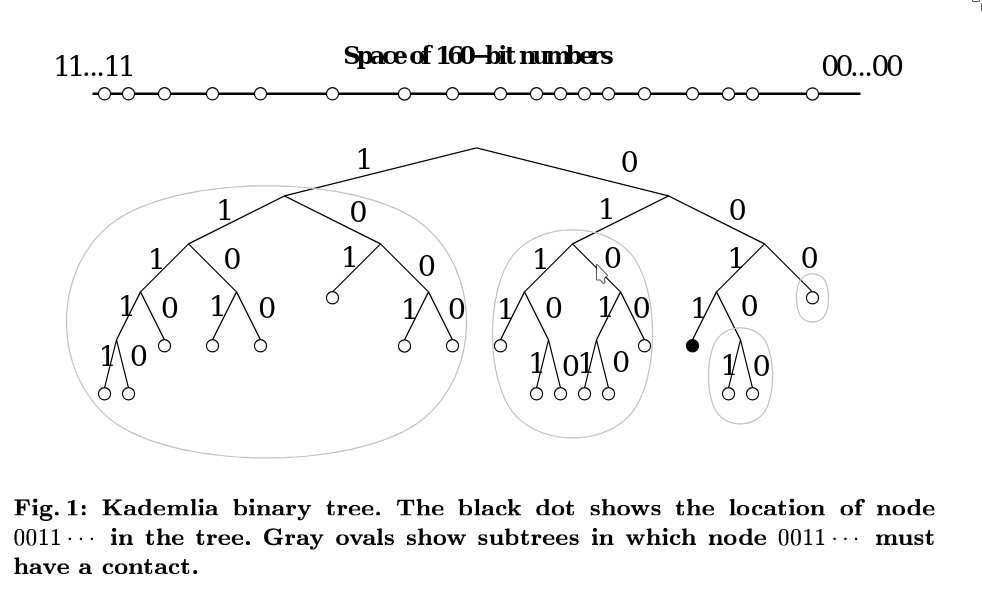
Kademlia ensures that every node knows at least one other node in each of its subtrees. This allows it to successively query the node that is closest to the desired target, continuing the process until it converges on the target node.

2.1 XOR Metric

Given two 160-bit identifiers, \(x\) and \(y\), Kademlia defines the distance between them as the bitwise exclusive OR (XOR), interpreted as an integer:

The XOR metric satisfies the four conditions of a proper metric: (i) symmetry, (ii) triangle inequality, (iii) the distance from a node to itself is zero, and (iv) positivity (distance is always non-negative, and only zero when \(x = y\)).

Furthermore, the XOR metric corresponds directly to the implicit binary tree structure each node uses. Specifically, the distance between two node IDs reflects the height of the smallest subtree containing both. If no such subtree exists, it corresponds to the subtree defined by the longest common prefix.

2.2 Node State

Every Kademlia node maintains a list of \(\langle \text{IP address}, \text{UDP port}, \text{Node ID} \rangle\) tuples for each bit \(i\) in the 160-bit ID space, i.e., \(0 \leq i < 160\). Each of these lists is called a k-bucket.

Each k-bucket is sorted with the least recently seen node at the head and the most recently seen node at the tail. This design helps defend against DDoS attacks: connections to older, long-lived nodes are preferred. This makes it harder for newly created or malicious nodes to flood the routing tables, and also improves reliability, as long-lived nodes are more likely to remain online.

When a Kademlia node receives any message from another node, it updates the appropriate k-bucket with that node’s information.

• If the node is already present, it is moved to the tail of the k-bucket (most recently seen).
• If the node is not present and the k-bucket has space, it is added to the tail.
• If the k-bucket is full, the current node pings the least recently seen node (the one at the head).
  • If that node is unresponsive, it is removed, and the new node is added.
  • If it is still responsive, the new node is dropped.

2.3 Kademlia Protocol

Kademlia consists of four core message types:

• PING: Checks whether a given node is still alive.
• STORE: Requests that a node store a given <key, value> pair.
• FIND_NODE: Takes a node ID as input and returns a list of up to k triples \(\langle \text{IP address}, \text{UDP port}, \text{Node ID} \rangle\) of the k closest nodes it knows to the target ID.
• FIND_VALUE: Behaves like FIND_NODE, but if the queried node has the value locally stored for the given key, it returns the value instead of node contact information.

Node lookups use the FIND_NODE operation in a parallel and asynchronous fashion. The querying node recursively contacts the \(\alpha\) closest nodes (where \(\alpha\) is a tunable parameter) to the target node ID. Nodes that fail to respond quickly are removed from consideration. If no closer nodes are found among the first \(\alpha\), the rest of the known nodes are queried.

Because of Kademlia’s behavior, repeated searches for the same key are likely to be cached at intermediate nodes. However, this could lead to over-caching of very popular keys, possibly resulting in every node storing them. To prevent this, each <key, value> pair is assigned an expiration time, which is inversely proportional (in an exponential way) to the number of nodes between the current node and the node whose ID is closest to the key.

2.4 Routing Table

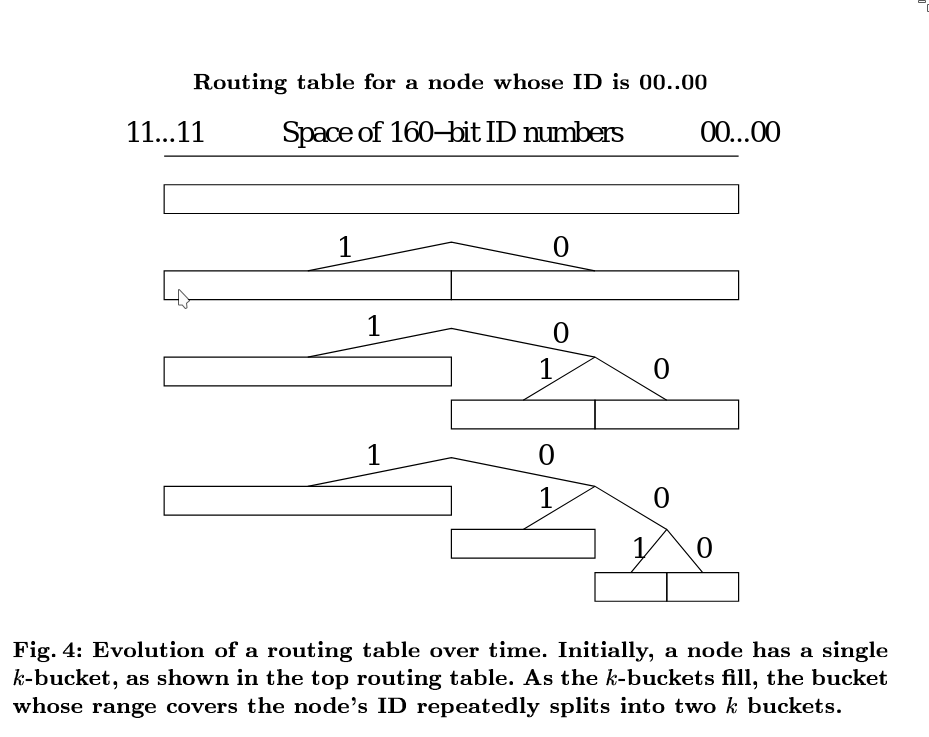
Kademlia’s routing table is organized as a binary tree, with its leaves representing k-buckets. Each k-bucket covers a specific range of the ID space.

Initially, a node’s routing table consists of a single k-bucket that covers the entire ID space. When the node learns about a new peer, it attempts to insert it into the appropriate k-bucket.

• If the bucket has space, the node is simply inserted.
• If the bucket is full, and the current node’s ID falls within the range of that bucket, the bucket is split into two smaller k-buckets.
  • The old entries are redistributed between the two new buckets based on their ID range.
  • The insertion is retried.

This splitting behavior ensures that a node knows more about nodes that are close to it in the ID space, enabling efficient and scalable routing.

2.5 Efficient Key Republishing

To ensure that <key, value> pairs persist over time, nodes must periodically republish their keys. This is necessary due to churn—nodes leaving and joining the network.

Kademlia republishes each <key, value> pair once per hour. A naïve republishing approach would generate a large number of messages, so Kademlia employs various optimizations to minimize network overhead while still maintaining data availability.

3. Implementation Notes

• To reduce traffic, Kademlia delays sending PING requests to check if a node is alive, unless it has a useful message to send to that node.
• Since Kademlia uses UDP, which is unreliable and may drop packets, it uses exponentially increasing backoff to retry failed messages.
• If a contact fails to respond to five consecutive messages, it is considered stale and may be removed from the routing table.
• To accelerate lookup, alternative tree structures can be used instead of a binary tree, such as a ternary tree or more generally an n-ary tree.

4. Conclusion

Kademlia, with its novel XOR-based metric, is a peer-to-peer system that is both consistent and high-performing. Its routing strategy, asynchronous design, and resilience to churn make it a robust choice for decentralized distributed hash tables.

reply via email