Layer Normalization

October 23, 2025 | 440 words | 3min read

Paper Title: Layer Normalization

Link to Paper: https://arxiv.org/abs/1607.06450

Date: 14. June 2016

Paper Type: Deep-Learning, Architecture, Training-Technique

Short Abstract: This paper introduces the layer normalization technique, which is an extra layer that can be placed between other layers to normalize their outputs. This helps stabilize training and reduces the time needed to train a model. In addition, unlike batch normalization, it works well with recurrent neural networks (RNNs).

1. Introduction

Deep neural networks trained with stochastic gradient descent have outperformed other techniques in supervised learning tasks. However, these deep networks often require many days of training. One technique used to speed up training is batch normalization, which normalizes over the batch size by calculating the mean and standard deviation. This not only allows for faster convergence but also acts as a regularization method.

However, batch normalization requires calculating the running average of the mean and standard deviation. While this works for networks with fixed input sizes, it becomes difficult for recurrent neural networks, which often have variable input lengths. Batch normalization also performs poorly when mini-batches are very small.

To address these limitations, the authors introduce layer normalization, which acts like a hidden layer. It not only works well for RNNs but also generalizes effectively across different architectures.

2. Background

One of the main problems in deep learning is that the gradients with respect to the weights, computed during backpropagation, are highly dependent on the outputs of neurons in the previous layer. Batch normalization was introduced to reduce this covariate shift.

3. Layer Normalization

Changes in the output of one layer tend to cause highly correlated changes in the summed input of the next layer—particularly when using ReLU activation functions. To address this, the authors propose fixing the mean and variance of the summed input of each layer.

Their idea is to compute layer normalization over all hidden units in the same layer as follows:

$$ \mu^l = \frac{1}{H} \sum_{i=1}^H a_i^l, \quad \sigma^l = \sqrt{\frac{1}{H} \sum_{i=1}^H (a_i^l - \mu^l)^2} $$

where ( H ) is the number of hidden units in the layer.

This approach also works well for RNNs. In recurrent networks, the average magnitude of the summed input in the recurrent unit tends to grow or shrink over time, leading to exploding or vanishing gradients. Since layer normalization is invariant to rescaling, it helps prevent these issues.

In summary:

• Batch normalization normalizes across the batch dimension.
• Layer normalization normalizes across the feature dimension.

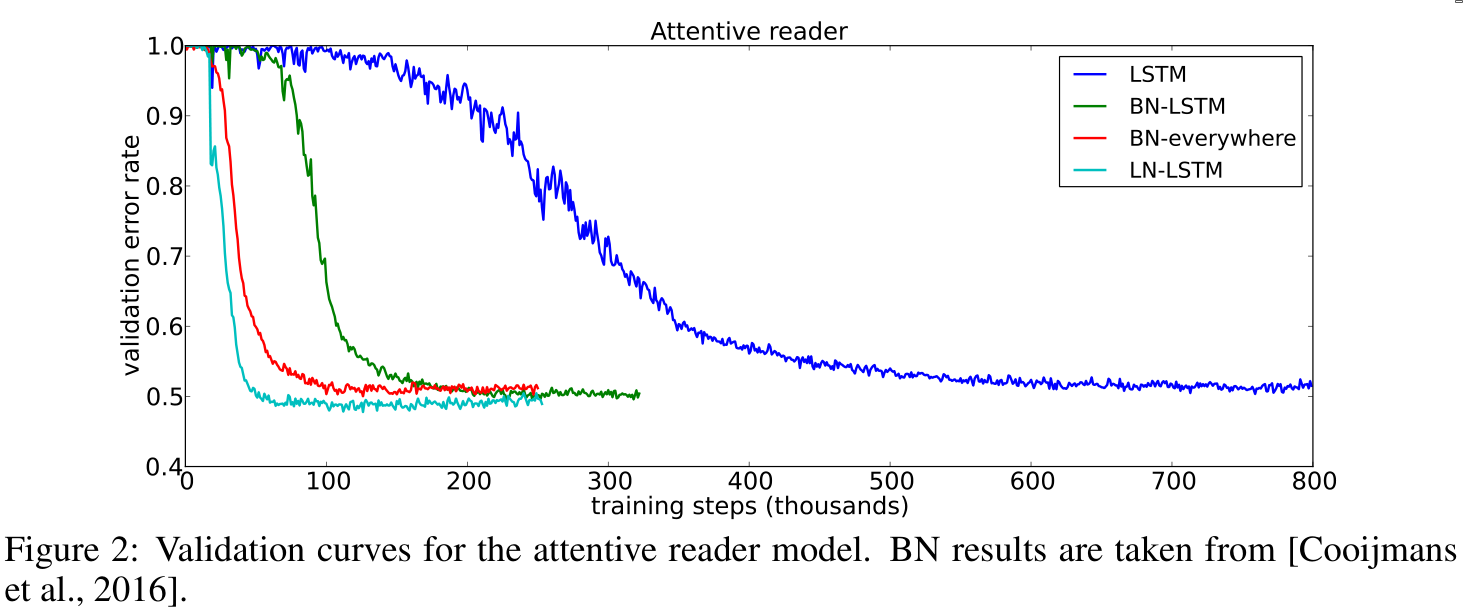
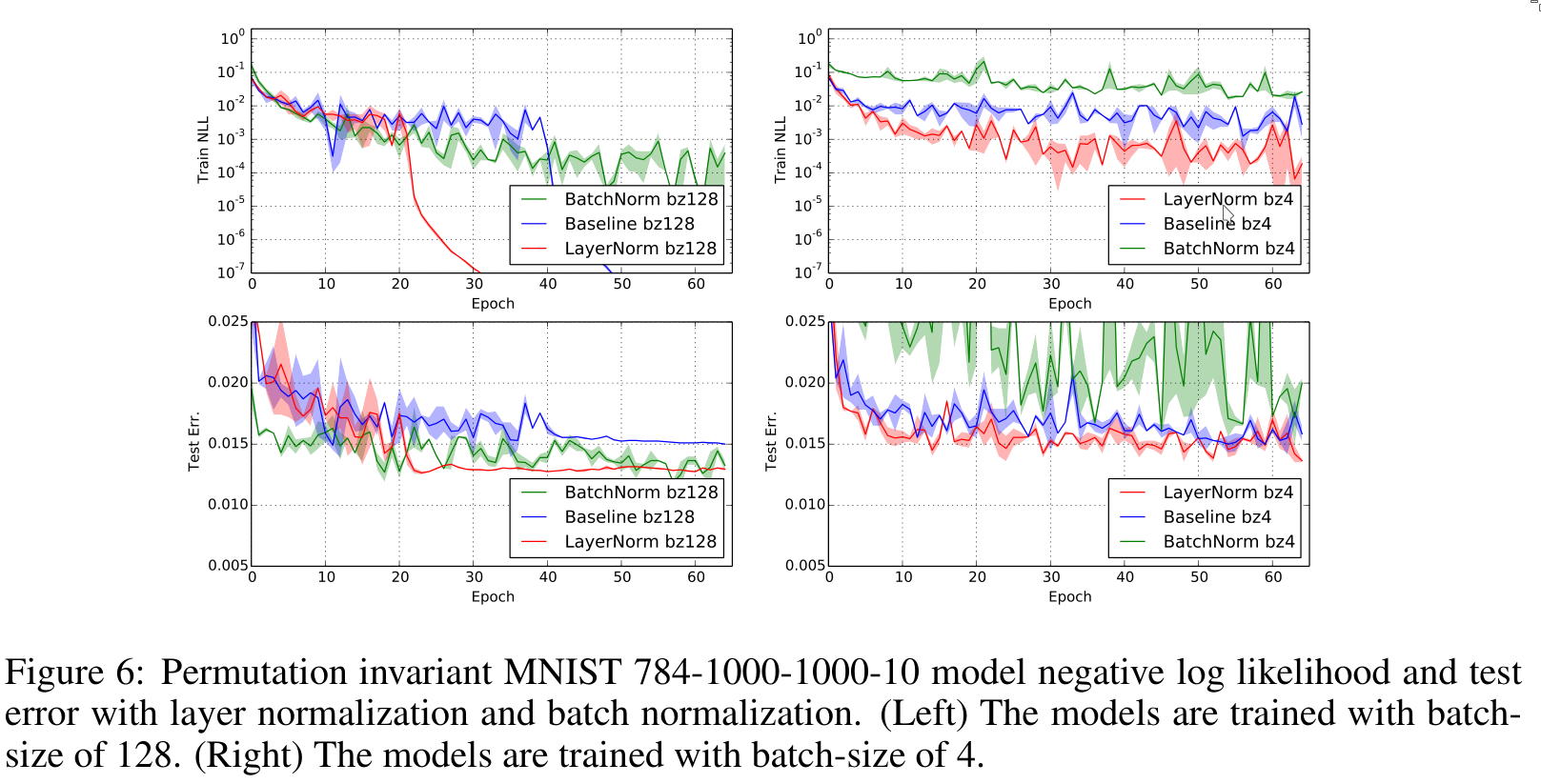
4. Experimental Results

The authors experiment with layer normalization on various NLP tasks.

5. Conclusion

Layer normalization helps speed up the training of neural networks. Its benefits are especially pronounced for long sequences and small mini-batches.