The LLM ARChitect: Solving the ARC Challenge Is a Matter of Perspective

December 2, 2024 | 675 words | 4min read

Paper Title: The LLM ARChitect: Solving the ARC Challenge Is a Matter of Perspective
Link to Paper: https://www.scribd.com/document/796451493/the-architects
Date: /
Paper Type: Deep Learning, ARC-Challange
Short Abstract:
The paper introduces a method powered by LLMS to solve the ARC challenge.

1. Introduction

LLMs have shown remarkable results across various benchmarks and disciplines. However, a fundamental question remains unanswered: “Can these systems truly reason?” The Abstraction and Reasoning Corpus (ARC) is specifically designed to test this capability.

Traditional systems have historically struggled with this benchmark, but recent advancements in language models have yielded promising results.

Notably, recent research suggests that the limitations of language models may stem more from their implementation rather than inherent shortcomings. One of the main culprits is tokenization, which often leads to deficits in reasoning.

In their paper, the authors present an LLM system that addresses these issues and successfully solves 72.5 tasks out of 100 in the ARC dataset.

2. Pipeline

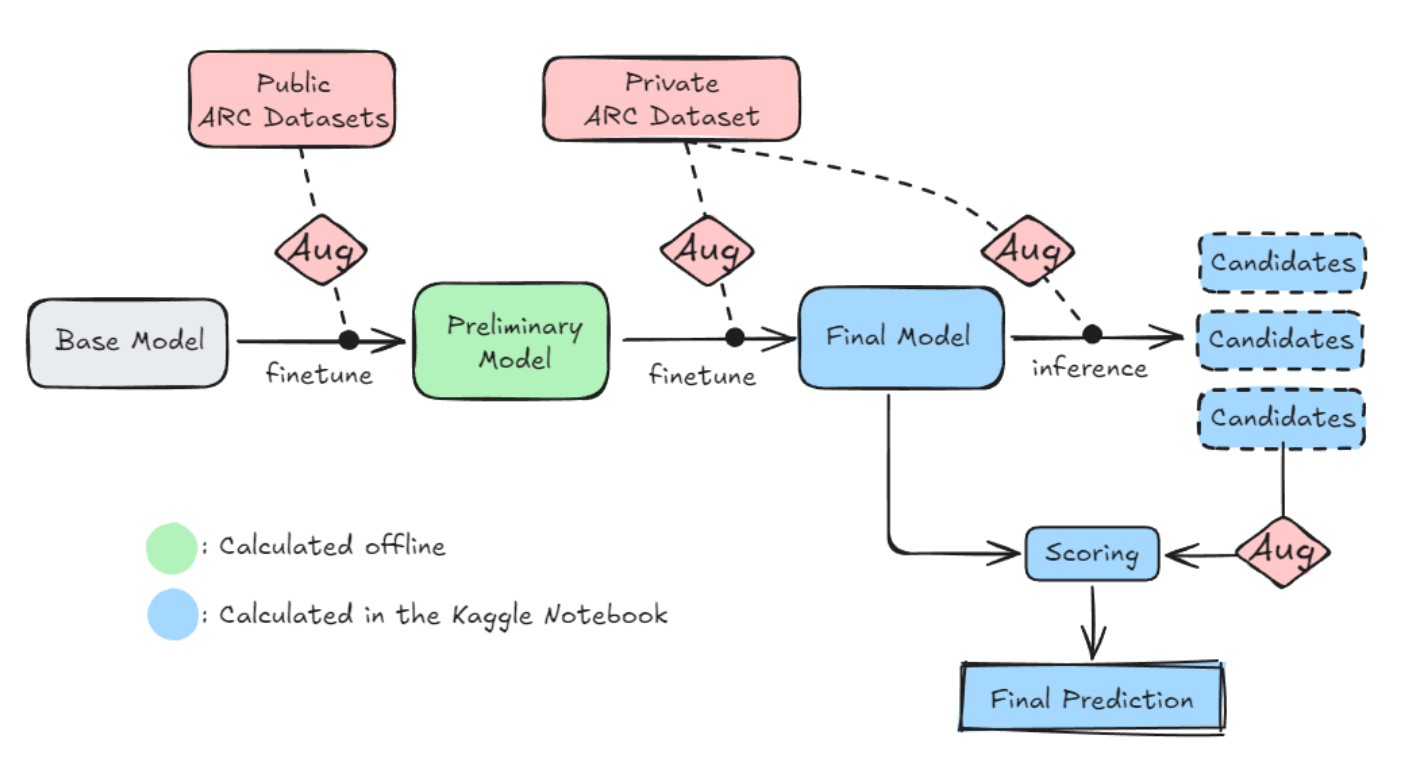
Key Components:

Instead of using the public ARC dataset, they utilized the expanded Re-ARC dataset, which was created through generators and is a superset of ARC.
They restricted the tokenizer of the language models to 64 tokens.
Various augmentations were applied to increase the dataset size, including rotations, transpositions, and permutations of colors.
For the LLM, they used the Mistral-NeMo-Minitron-8B-Base model as the foundation, which they later fine-tuned with their dataset.
After fine-tuning, they generated multiple solution candidates. These candidates were sampled using their custom algorithm, which employs depth-first search.
Finally, they selected the candidate with the highest aggregated log softmax score.

3. Method

3.1 Dataset

The ARC dataset consists of 900 reasoning tasks, divided into 400 training tasks and 400 evaluation tasks.

Each task involves grids of varying sizes, ranging from 1x1 to 30x30, and utilizes a palette of colors.

Each task contains multiple instances, where each instance comprises two grids: one representing the input of the problem and the other the expected output.

The objective of the system is to determine the underlying mechanism governing the instances in a given task and produce the expected output.

Two examples of ARC tasks, each having multiple instances, consisting of an input and output grid pair.

3.2 Data Modeling

Many failure modes of LLMs arise from poor tokenization, such as when successive digits are grouped together incorrectly.

To address this, the authors decided to limit the tokenizer to 64 tokens, ensuring that characters are not grouped inappropriately.

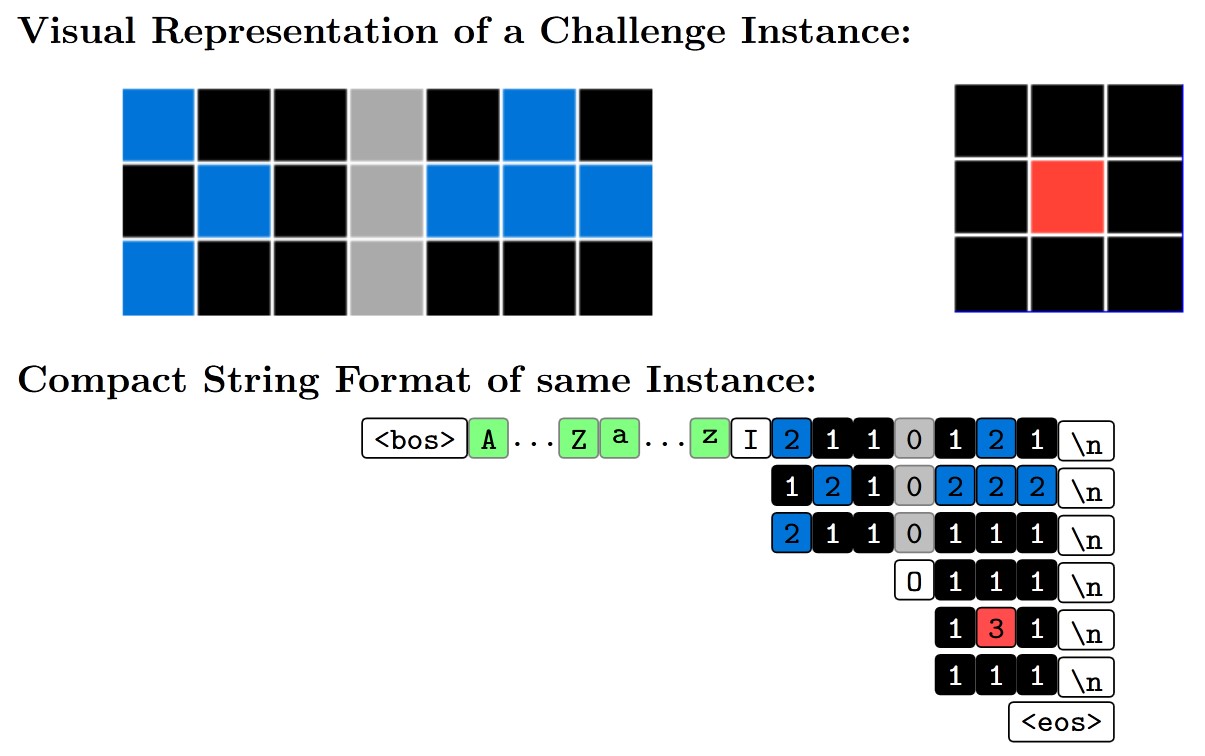
Additionally, they introduced various characters at the beginning of the input problem representation. This strategy provided the LLM with additional “thinking time” and allowed it to use tokens as a computational buffer, significantly improving accuracy.

3.3 Training the Model

The authors used the Mistral-NeMo-Minitron-8B-Base model and, due to memory constraints, employed LoRa with 4-bit quantization and gradient checkpointing.

3.4 Solution Inference

For inference, tokens can be generated either greedily or stochastically. Tokens are produced until the <eos> token, which marks the end of an example.

However, both greedy and stochastic sampling yielded poor results. To improve this, the authors devised their own technique.

They utilized depth-first search (DFS) to explore possible paths in the token tree and stopped exploring paths where the cumulative probability fell below 5%.

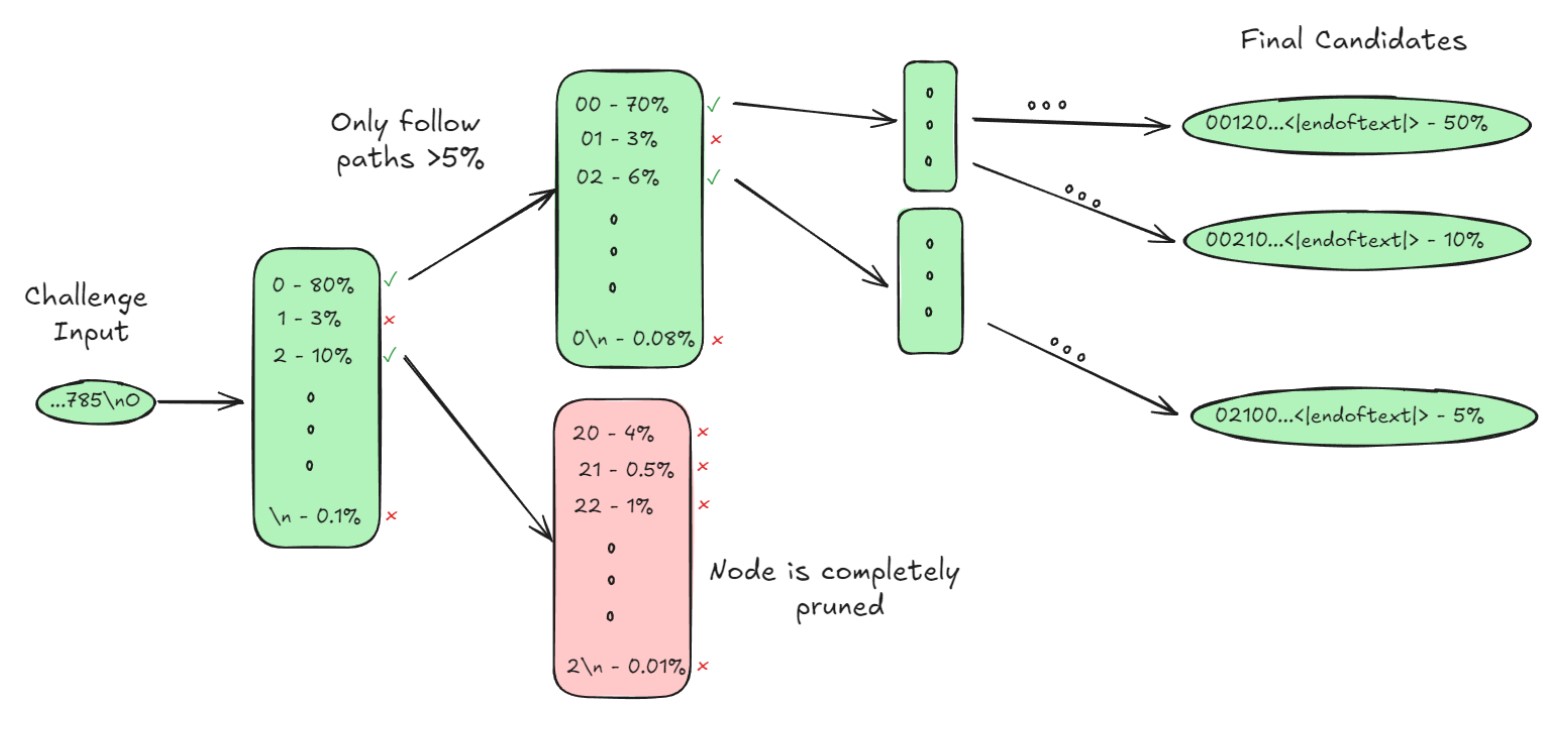
Sampling using the DFS algorithm: only paths with cumulative probabilities greater than 5% are explored.

3.5 Selection Strategy

After generating a list of candidates, one candidate must be selected as the final result.

To achieve this, the authors calculated the cumulative probability for each candidate across augmented problem instances. Specifically, they determined the likelihood of the token sequence for a candidate in multiple augmented instances and summed these probabilities.

The final solution was chosen as the candidate with the highest accumulated probability.

The rationale behind this process is that the correct solution should be the most robust against augmentations.

4. Conclusion

The most significant contributions of this paper were the tokenization approach using a reduced token set, the modeling of input with these tokens, and the innovative sampling and selection strategy for determining the solution from candidate outputs.