Mathematical discoveries from program search with large language models

Published: February 4, 2024

Paper Title: Mathematical discoveries from program search with large language models
Link to Paper: https://www.nature.com/articles/s41586-023-06924-6
Date: 14. December 2023
Paper Type: LLM, RL, Coding
Short Abstract:
The authors of this paper introduce FunSearch, an evolutionary algorithm using LLM with an evaluator to solve combinatoric problems and make new mathematical discoveries. This marks the first instance where novel mathematical knowledge was uncovered through the assistance of a language model.

1. Introduction

Numerous NP-Problems are challenging to solve, yet they possess a polynomial evaluation algorithm. This paper focuses on such problems, aiming to generate solve programs that receive high scores from the polynomial evaluator.

Creating effective solve programs requires exploration of new ideas, a task complicated by LLMs’ susceptibility to “hallucinations.” Recent approaches have sought to mitigate this issue by integrating LLMs with evolutionary methods.

FunSearch (short for “searching in the function space”) combines a pre-trained LLM, tasked with generating creative programs, with an evaluator that ranks the generated programs, minimizing the impact of hallucinations.

The essence of FunSearch lies in sampling the best-performing programs and feeding them back to the LLM via prompts. It begins with a program skeleton containing simple boilerplate code and iterates only the critical logic part. Throughout iterations, a diverse program pool is maintained using an island-based approach.

The authors apply FunSearch to various combinatoric problems, leading to the discovery of new mathematical knowledge.

FunSearch doesn’t generate a solution, it produces programs generating the solution.

2. FunSearch

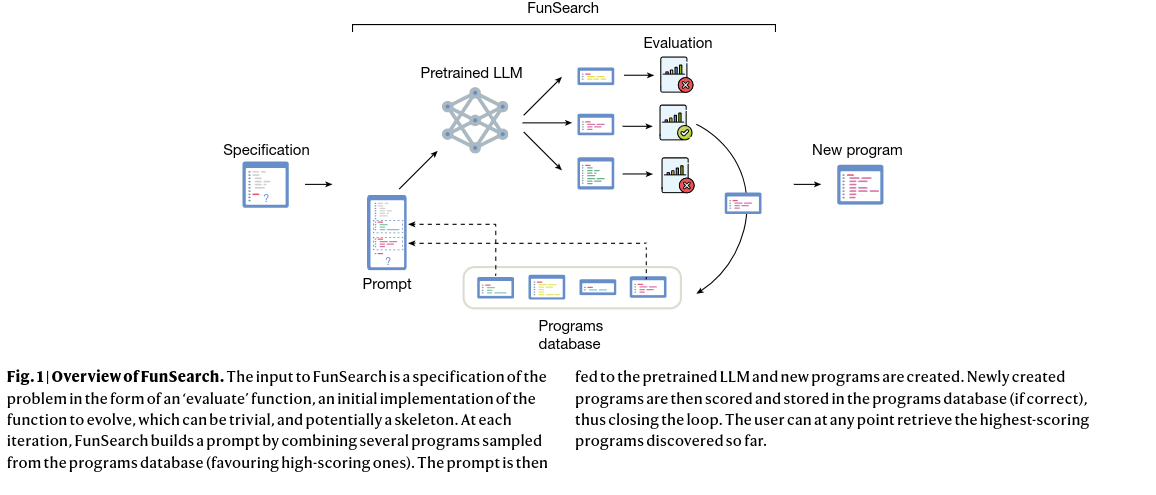
Figure 1 provides an overview of the FunSearch algorithm. The subsequent sections elaborate on the individual modules of the algorithm.

Specification The FunSearch algorithm takes the problem’s specification as input, consisting of code with three parts: the evaluate function (used to score generated programs), the logic function (the function that gets evolved and the core of the solve program), and the boilerplate code (specifying how the logic and evaluate functions will be used). FunSearch evolves the logic function, the most challenging part to develop. The authors found that providing the algorithm with a rudimentary naive solve program and a doc string with additional information speeds up the discovery of improved solve programs.

Pre-trained LLM The LLM is the creative core of FunSearch, tasked with enhancing the logic function and creating the solve program. The authors use Codey as their LLM, built upon the PaLM model. They note that other LLMs can also be employed.

Evaluation Generated programs undergo evaluation and scoring based on different dimensions such as speed and space complexity. Scores across dimensions are combined into an overall score using the mean. Programs that failed to execute or were incorrect are discarded, while the remaining programs are sent to the program database.

Programs database The programs database maintains a population of correct programs, encouraging the creativity of the LLM by keeping track of diverse solve algorithms. Multiple islands (populations) ensure diversity. Programs using shorter code are favored, and the worst half of solve algorithms in an island are periodically replaced by a new population, cloned from another island.

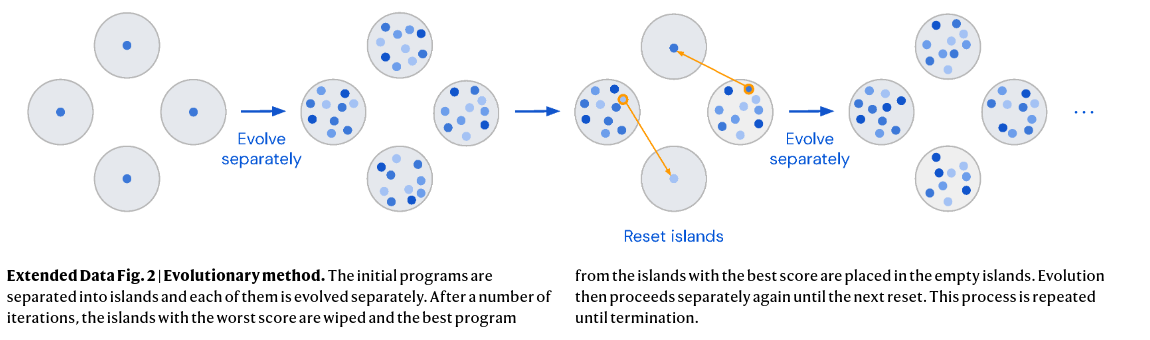
Prompt To generate new solve programs, the LLM is fed with $k$ programs from the program database. Sampled programs are sorted by score and assigned version numbers before being combined into a single prompt. This is done so that the LLM knows which solve programs are better.

3. Results

3.1 Extremal combinatorics

Extremal combinatorics study the maximal (or minimal) possible sizes of sets satisfying certain properties.

Cap sets Refers to the task of finding the largest possible set of vectors in $\mathbb{Z}_3^{n}$ such that no three vectors sum to zero.

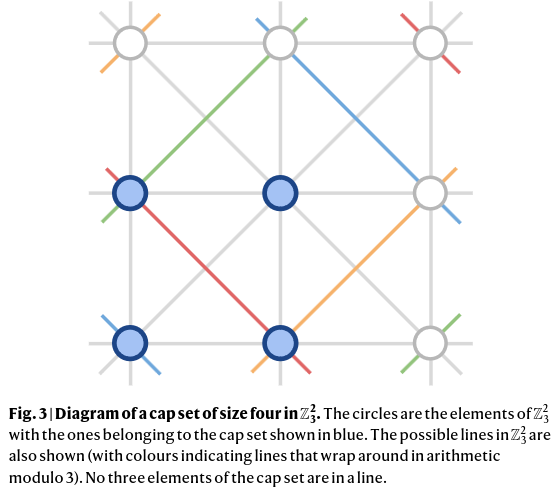
In dimension n = 8, FunSearch found a larger cap set than what was previously known.

3.2 Bin packing

The goal of bin packing is to pack a set of items of various sizes into the smallest number of fixed-sized bins.

Several online algorithms for bin packing have strong worst-case performance but often fall short in practice. FunSearch identified a heuristic superior to commonly used algorithms.

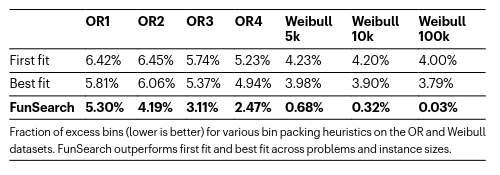
FunSearch discovers a better heuristic than commonly used algorithms.

4. Conclusion

FunSearch is effective in discovering new knowledge for hard problems. The LLM provides suggestion that marginally improve the existing results, and over time find a good solve program.