Deep Residual Learning for Image Recognition

October 28, 2025 | 422 words | 2min read

Paper Title: Deep Residual Learning for Image Recognition

Link to Paper: https://arxiv.org/abs/1512.03385

Date: 10. Dec. 2015

Paper Type: Architecture, Learning Techniques, Deep Learning

Short Abstract: Deeper networks are harder to train than shallower networks. In this paper, the authors introduce the technique of adding residual connections to the network, which drastically improves the performance of deeper networks.

1. Introduction

Deep neural networks — that is, networks with many layers — have been used in many breakthroughs in machine learning. This raises the question: Is learning better networks as easy as stacking more layers?

One problem that arises when stacking more layers is that of vanishing and exploding gradients, but this can be more or less solved by techniques such as batch normalization and normalization layers.

Another problem when stacking more layers is that of degradation: with ever-increasing depth, the accuracy becomes saturated, and the network no longer improves.

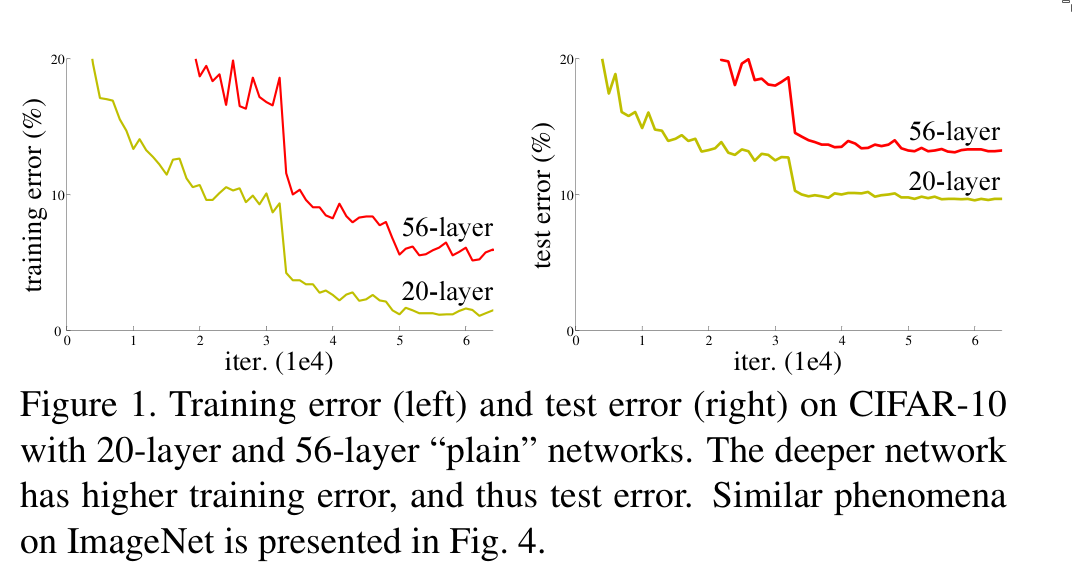
If we have a shallower network that provides better accuracy than a deeper one, and we add layers to the shallow network that are identity functions, then the deeper network should never produce a higher training error than the shallower one.

But apparently, current optimizers seem unable to find this solution. Hence, the authors propose adding deep residual connections between layers.

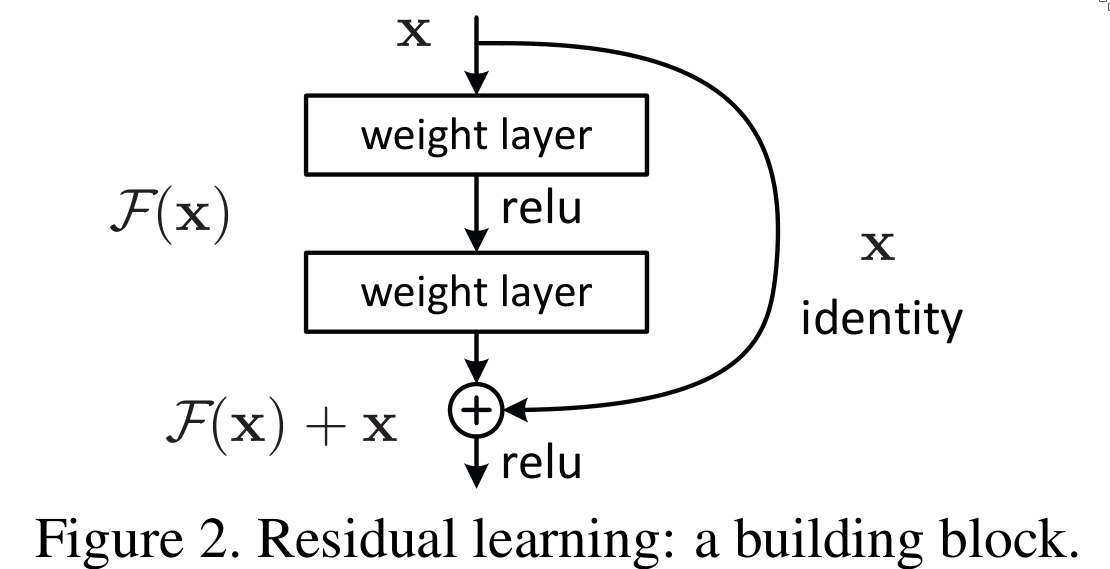
These shortcut connections can be realized simply by performing identity mapping, and their outputs are added to the output of the stacked layers. More formally:

$$ y = F(x, W) + x $$

2. Deep Residual Learning

The idea is that instead of expecting the stacked layers to approximate the function \(H(x)\), which represents the underlying mapping of several stacked layers, they let the stacked layers approximate the residual function:

$$ F(x) := H(x) - x $$

This formulation is motivated by the degradation phenomenon, which suggests that deeper networks have difficulty approximating the identity function.

In reality, using the identity function is probably not the optimal state, but it provides good preconditioning from which the network can start: it begins with an identity mapping and then learns how to adjust it to fit the task.

A residual block is defined as:

$$ y = F(x, W) + x $$

If the dimensions do not match, zero-padding can be used, or a linear projection can be performed:

$$ y = F(x, W) + W_s x $$

3. Experiments

Experiments were done using ImageNet 2012. For the architecture of the network, 18-layer and 34-layer networks were used, both with and without residual connections.

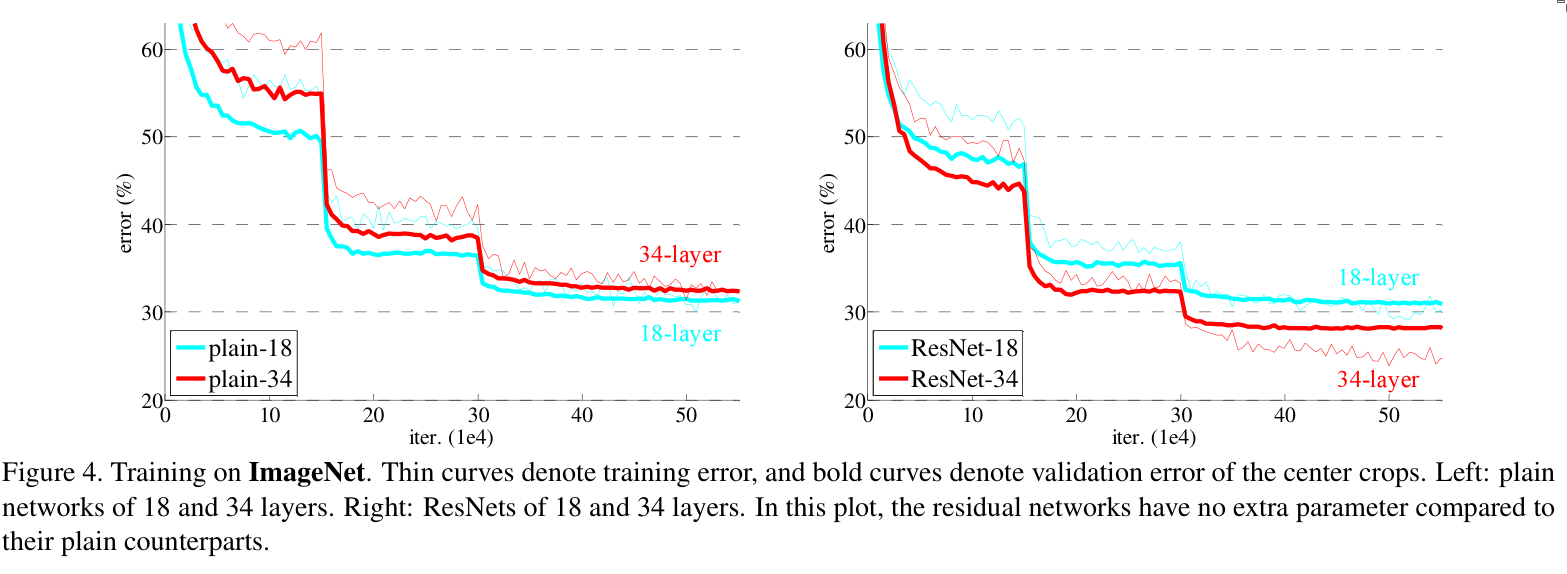
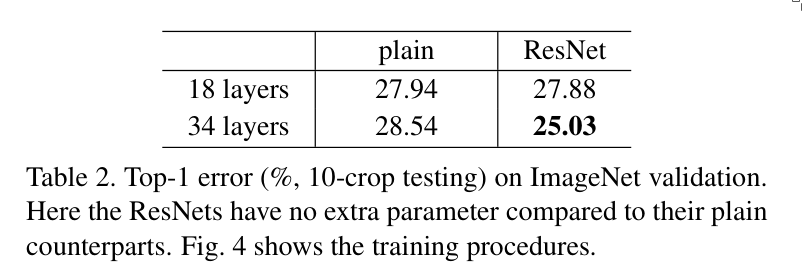
4. Conclusion

Deep Residual Networks help deeper networks improve their convergence speed and overall performance.