Simple framework for constructing functional spiking recurrent neural networks

October 1, 2025 | 412 words | 2min read

Paper Title: Simple framework for constructing functional spiking recurrent neural networks

Link to Paper: https://www.pnas.org/doi/10.1073/pnas.1905926116

Date: 21 Oct. 2019

Paper Type: Spiking-RNN, Continuous-time-RNN, Converting

Short Abstract: In this paper, the authors present a technique to accurately convert a continuous-variable rate RNN into a spiking RNN.

1. Introduction

Training spiking networks is often difficult due to the non-differentiable nature of spike signals, which prevents the use of gradient descent via backpropagation.

Meanwhile, training a continuous-variable rate RNN is much more straightforward and can easily be done using gradient descent.

Hence, the authors first train a continuous-variable rate RNN and then map it to a spiking RNN using leaky integrate-and-fire (LIF) units, without significant compromise in task performance.

2. Method

2.1 Model

The continuous-variable rate network model consists of (N) rate units, whose output is obtained through a nonlinear transfer function based on firing rate encoding.

The spiking RNN is a network composed of (N) LIF units.

The implementation can be found here.

2.2 Training

To train the continuous RNN, the authors use backpropagation through time (BPTT).

As training data/benchmarks, Go/No-Go tasks are used.

2.3 Mapping from Continuous RNN to Spiking RNN

In their framework, the three sets of weight matrices \((W_{in}), (W_{rate}), and (W_{rate}^{out})\), along with the tuned synaptic time constants \((\tau_d)\) from a trained rate RNN, are transferred to a network of LIF spiking units.

The spiking RNN is initialized with the same topology as the rate RNN. The input weight matrix and synaptic time constants are directly transferred without modification, but the recurrent connectivity and readout weights need to be scaled by a constant factor \((\lambda)\) to account for differences in firing rate scales between the rate model and the spiking model.

With an appropriate value of \(\lambda\), the LIF network performs the task with the same accuracy as the rate network. The scaling factor \(\lambda\) is determined via a grid search method.

3. Results

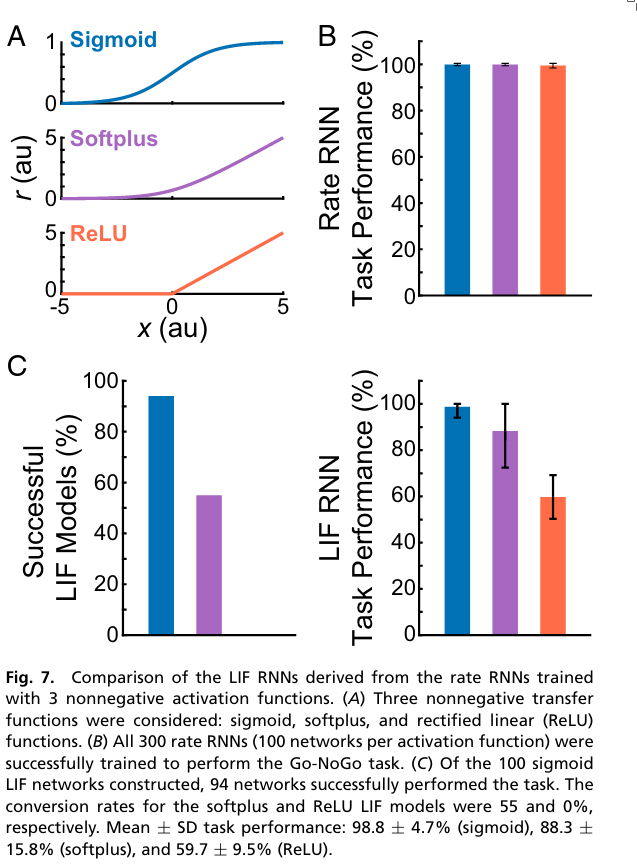
One of the most important factors determining whether rate RNNs can be mapped to LIF RNNs in a one-to-one manner is the nonlinear transfer function used in the rate models.

The average task performance and the number of successful LIF RNNs were highest for rate models trained with the sigmoid transfer function.

4. Conclusion

Their transformation works.

reply via email