Notes from the Wired

Time, Clocks, and the Ordering of Events in a Distributed System

May 13, 2025 | 1,275 words | 6min read

Paper Title: Time, Clocks, and the Ordering of Events in a Distributed System
Link to Paper: https://lamport.azurewebsites.net/pubs/time-clocks.pdf
Date Published: July 1978
Paper Type: Decentralized Systems, Distributed Architectre, Process Synchronisation
Short Abstract:
This paper uses local “clocks” in the processes of an asynchronous distributed system to derive a total order from the happened-before relation. This approach is used to solve the problem of mutual exclusion for accessing shared resources, i.e., critical sections.

1. Introduction

Time is an important concept when discussing whether one event happened before another. However, in distributed systems, it is often difficult to maintain a single, globally consistent time.

A distributed system consists of multiple distinct processes that are spatially separated and communicate with each other, for example, the ARPANET.

In such distributed systems, it is often impossible to determine a global order of events. As a result, the happened-before relation only forms a partial ordering.

This paper proposes a method to extend this partial order to a total order, using an algorithm that can be applied to solve synchronization problems such as mutual exclusion.

2. The Partial Order

Assumptions:

Definition: The relation \(\rightarrow\) (read as “happened before”) defined on the set of events in the system satisfies the following conditions:

  1. If \(a\) and \(b\) are events in the same process and \(a\) occurs before \(b\), then \(a \rightarrow b\).
  2. If \(a\) is the sending of a message by one process and \(b\) is the receipt of that message by another process, then \(a \rightarrow b\).
  3. If \(a \rightarrow b\) and \(b \rightarrow c\), then \(a \rightarrow c\) (transitivity).

Two distinct events \(a\) and \(b\) are said to be concurrent if \(a \not\rightarrow b\) and \(b \not\rightarrow a\).

This relation can be visualized using a space-time diagram. In such diagrams:

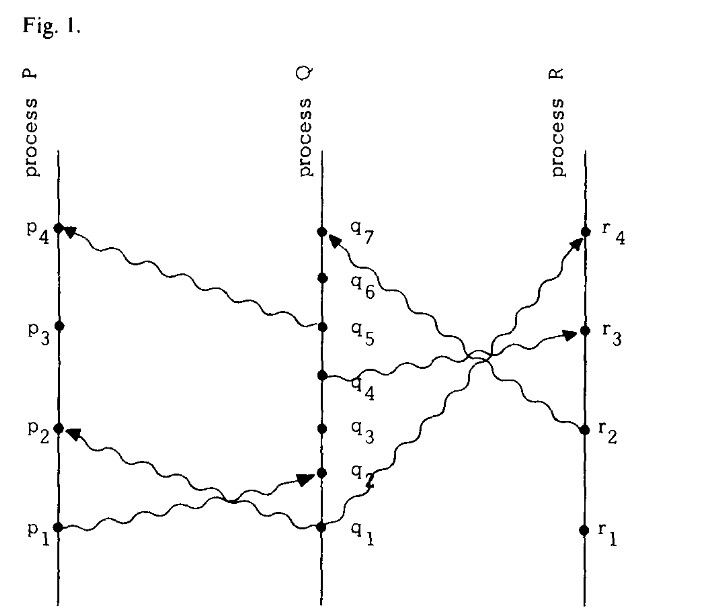
Another way to interpret \(a \rightarrow b\) is to say that event \(a\) could causally affect event \(b\). Two events are concurrent if neither can influence the other. For example, events \(p_3\) and \(q_3\) in Figure 1 are concurrent.

3. Logical Clocks

To introduce ordering in the system, we define logical clocks:

To maintain a correct logical clock system, we enforce the following Clock Conditions:

  1. If \(a\) and \(b\) are events in the same process \(P_i\), and \(a\) comes before \(b\), then \(C_i(a) < C_i(b)\).
  2. If \(a\) is the sending of a message by process \(P_i\) and \(b\) is the receipt of that message by process \(P_j\), then \(C_i(a) < C_j(b)\).

Now, let us consider that the processes are algorithms and events are the steps during their execution. To satisfy the clock conditions, we must follow these Implementation Rules:

  1. Increment Rule: Each process \(P_i\) increments its clock \(C_i\) between any two successive events.

  2. Message Rule: (a) If an event \(a\) is the sending of a message \(m\) by process \(P_i\), then \(m\) includes a timestamp \(C_i(a)\). (b) Upon receiving message \(m\) with timestamp \(T_m\), process \(P_j\) sets its clock to at least \(\max(C_j, T_m) + 1\).

This second rule ensures that the receiving process’s logical clock reflects the causality introduced by the message, thus satisfying the clock conditions and maintaining a consistent logical time across the distributed system.

4. Ordering the Events Totally

Using the previously defined clock conditions and implementation rules, we can now construct a total ordering of events by simply ordering them based on the timestamps assigned by the logical clocks.

More precisely: If \(a\) is an event in process \(P_i\) and \(b\) is an event in process \(P_j\), then we say \(a < b\) if and only if:

  1. \(C_i(a) < C_j(b)\), or
  2. \(C_i(a) = C_j(b)\) and \(P_i < P_j\) (a tie-breaker based on process IDs).

This gives us a total ordering of events that extends the happened-before partial order.

4.1 Why is this total ordering useful?

Suppose we have a fixed set of processes that share a single resource, and only one process may use the resource at a time. We want to design an algorithm that satisfies the following three conditions:

  1. A process that has been granted the resource must release it before the resource can be granted to another process.
  2. Requests for the resource must be granted in the order in which they were made.
  3. If every process that is granted the resource eventually releases it, then every request is eventually granted.

This is a non-trivial problem. In centralized systems, it’s typically solved using a global physical clock. However, in a distributed system, no such global clock exists.

Example: Suppose process \(P_1\) sends a request to \(P_0\) and then sends a message to \(P_2\). Upon receiving the message, \(P_2\) sends its own request to \(P_0\). It’s possible for \(P_2\)’s request to arrive at \(P_0\) before \(P_1\)’s, violating condition (2), since the system can’t infer the causal relation between the two requests.

4.2 Solution: Distributed Mutual Exclusion Algorithm

We solve this using the following algorithm:

  1. To request the resource, process \(P_i\) sends the message T_m: P_i requests resource to every other process and adds the message to its own request queue. Here, \(T_m\) is the timestamp assigned by \(P_i\)’s logical clock.

  2. When process \(P_j\) receives the message T_m: P_i requests resource, it adds it to its own request queue and sends a timestamped acknowledgment back to \(P_i\).

  3. To release the resource, \(P_i\) removes the T_m: P_i requests resource message from its request queue and sends a timestamped release message to every other process: P_i releases resource.

  4. When process \(P_j\) receives a P_i releases resource message, it removes any matching request from its queue.

  5. Process \(P_i\) is granted the resource when:

    • (i) Its request is at the front of its request queue, meaning it is ordered before any other request according to the total order.
    • (ii) It has received an acknowledgment from every other process with a timestamp greater than \(T_m\).

This algorithm is fully distributed: each process independently follows the protocol, and there is no central coordinator or shared memory.

The algorithm can also be formalized using a state machine that runs on each processor.

5. Anomalous Behavior

Consider a nationwide system of interconnected computers. Suppose a person issues request A on computer A, then telephones a friend in another city, who issues request B on computer B. It is possible for request B to receive a lower timestamp than A, and therefore to be ordered before A in the system — even though, in real-world time, A happened before B.

This occurs because the system has no knowledge of external events (like phone calls), and it cannot infer causal relationships outside of message-passing within the system.

5.1 How can we avoid such anomalies?

There are two possible solutions:

  1. Manual Coordination: The user who issues request A can obtain its timestamp \(T_A\). When the friend issues request B, they can specify that B should be given a timestamp later than \(T_A\). This puts the responsibility on users to avoid anomalous ordering.

  2. Physical Clocks: Alternatively, if physical clocks are available and synchronized (to a reasonable degree), the system can assign timestamps based on real-world time, helping to prevent such anomalies. However, this introduces its own complexities and is not always practical in distributed environments.

Email Icon reply via email
▲
Made with Hugo, website licensed under CC BY-NC-SA 4.0.